Die nicht mit den unter Kapitel 1.2 (gerade Rohrleitungen, Krümmer, Querschnittsveränderungen,Verzweigungen) aufgeführten strömungstechnischen Zusammenhängen berechenbaren Kühlkreislaufeinzelwiderstände wie Motor, Kühler, Thermostat, Ölwärmetauscher usw. werden experimentell mit einem Prüfstandsaufbau zur Ermittlung der Bauteilwiderstände (siehe Kapitel 1.2) ermittelt.
Das Widerstandsverhalten einiger Bauteile eines PKW – Kühlkreislaufes zeigen folgende Bilder:
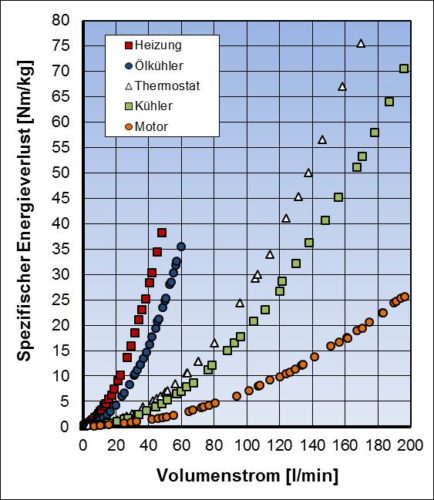
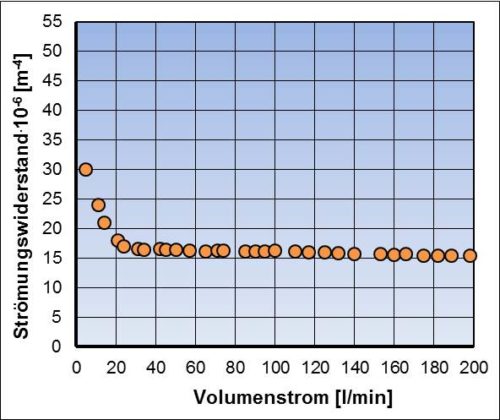
Oben links die spezifischen Energieverluste von ausgewählten PKW-Kühlkreislaufbauteilen und rechts diese Bauteilenergieverluste umgerechnet auf die jeweiligen Strömungswiderstände.
Bei beiden Darstellungen ist deutlich zu sehen, dass z.B. das Thermostat einen wesentlich größeren Strömungswiderstand aufweist als z.B. der gesamte Motor und auch als der Kühler. Im Sinne von Leistungs- und Bauraumeinsparung an der Kühlmittelpumpe, aber auch Verringerung von Bauteildruckbelastung und ggf. Kavitationsneigung ergibt sich damit hohes Druckverlusteinsparpotential. Bei Thermostatneuentwicklungen ist also auf kleine Druckverluste zu achten.
Hier nochmals die mathematischen Zusammenhänge zwischen Druckverlust, spezifischer Energieverlust, Strömungswiderstand, Strömungswiderstandsbeiwert und Reynoldszahl:
spezifischer Energieverlust:
![\[\boldsymbol {Y_{V}=\frac{\Delta p_{ges}}{\varrho}=R \cdot \dot{V}^{2}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-5c2624b240b048fde57a2930a009845e_l3.png "Rendered by QuickLaTeX.com")
Strömungswiderstand:
![\[\boldsymbol {R=\frac{\Delta p_{ges}}{\varrho \cdot \dot{V}^2}=\frac{Y_V}{\dot{V}^2}=\frac{\zeta}{2 \cdot A^{2}}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-96ecb2b5a916613c45735318ec7c0372_l3.png "Rendered by QuickLaTeX.com")
Strömungswiderstandsbeiwert:
![\[\boldsymbol {\zeta=\frac{2\cdot\Delta p_{ges}}{\varrho \cdot c^{2}}=R\cdot 2\cdot A^{2}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-b3f253ab004e56d5c0748f9722aa2c9e_l3.png "Rendered by QuickLaTeX.com")
Reynoldszahl:
![\[\boldsymbol {Re=\frac{\varrho \cdot c \cdot d}{\eta}=\frac{c\cdot d}{\nu}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-bcf6d0c2e2d72200384acd58924096c0_l3.png "Rendered by QuickLaTeX.com")
Zur Berechnung des spezifischen Energieverlustes wird also lediglich der Bauteildruckverlust nach Bernoulli (Gesamtdruckverlust) durch die Fluiddichte dividiert. Für den Strömungswiderstand wird der Energieverlust durch den Volumenstrom ins Quadrat dividiert (quadratische Abhängigkeit) und für den dimensionslosen Strömungswiderstandsbeiwert (Zeta-Wert) der Strömungswiderstand mit 2 und dem Strömungsquerschnitt ins Quadrat multipliziert.
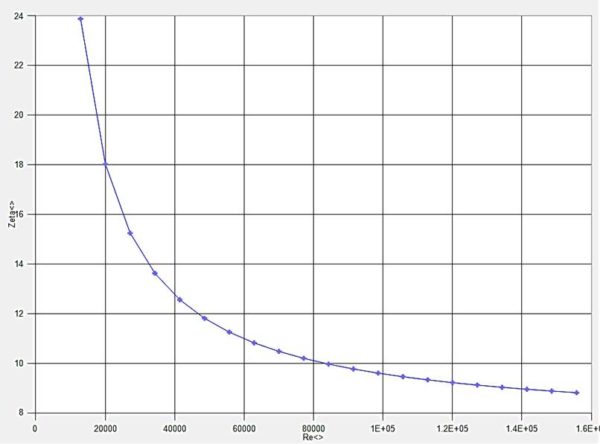
Nachfolgendes Diagramm zeigt den Verlauf des Strömungswiderstandsbeiwertes, dem sog. Zeta-Wert, eines Kühlkreislaufbauteiles in Abhängigkeit von der Reynoldszahl. Die Darstellung ist aus einer für einen konkreten Kühlkreislauf angefertigten Kreislaufberechnung in Flowmaster 7 entgenommen. Zu beachten ist bei diesen oft verwendeten Zeta-Wert-Kurven, dass zur Rückrechnung in einen Bauteildruckverlust die exakt bei der Zeta-Wert- und Reynoldszahl-Berechnung verwendete Strömungsfläche einzugeben ist! Ansonsten wird die gesamte Kreislaufberechnung fehlerhaft. Die Schwierigkeit zur Eingabe einer korrekten Strömungsfläche bei Verwendung des Zeta-Wertes zeigt sich, wenn ein Bauteil am Eingang und am Ausgang unterschiedliche Strömungsflächen aufweist, z.B. am Thermostat Richtung Kurzschlussleitung. Dann muss eine Festlegung getroffen werden, für welche Stelle die Strömungsfläche gilt. Für die andere Fläche stimmt dann aber zumindest die Reynoldszahl nicht.
Der Verlauf der Kennlinie des Zeta-Wertes ähnelt dem Kurvenverlauf bei Verwendung des Strömungswiderstandes R. Vorteil des R-Wertes ist, dass er im Gegensatz zum Zeta-Wert für alle Strömungsquerschnitte bzw.-flächen gilt (bei der Berechnung des Gesamtdruckes nach Bernoulli müssen zur Ermittlung des R-Wertes natürlich auch die dynamischen Druckanteile korrekt verwendet werden), Vorteil des Zeta-Wertes ist seine Dimensionslosigkeit.
Die Darstellungen sowohl vom Strömungswiderstand R als auch vom Strömungswiderstandsbeiwert Zeta zeigen deutlich, dass bei kleinen Kühlmittelvolumenströmen bzw. Reynoldszahlen der Strömungswiderstand stark ansteigt. Dieses Widerstandsverhalten der Einzelbauteile gilt auch für den Gesamtströmungswiderstand des Kühlkreislaufes, beispielhaft dargestellt im unteren Bild (ein Zeta-Wert für einen Gesamtkreislauf zeigt einen ähnlichen Verlauf):
Für einen Kühlkreislauf mit einer von der Kurbelwelle angetriebenen mechanischen Kühlmittelpumpe bedeutet dieser Verlauf des Gesamtströmungswiderstandes, dass im unteren Motordrehzahlbereich die Proportionalitätsbeziehungen für Kreiselpumpen (siehe auch Kapitel 4) nicht gelten und ein unterproportionaler Kühlmittelvolumenstrom gefördert wird. Daraus können Kühlungsprobleme in diesem Motorbetriebsbereich resultieren, besonders wenn zur Kraftstoff-einsparung die Motorleerlaufdrehzahl immer weiter abgesenkt wird. Für höhere Motordrehzahlen können die Proportionalitätsgesetze überschläglich zur Berechnung von Volumenströmen, Drücken und Verlustleistungen angewendet werden.