Die Kennlinien einer Kreiselpumpe lassen sich mittels Proportionalitätsgesetzen auf andere Drehzahlen umrechnen. Dies erklärt sich aus folgenden Verhältnissen am Schaufelrad:
Ändert man bei einer Pumpe, welche für eine bestimmte Förderleistung konzipiert wurde, die Drehzahl, so verändert sich auch die Umfangsgeschwindigkeiten am Eintritt von ![]() auf
auf ![]() und am Austritt von
und am Austritt von ![]() auf
auf ![]() .
.
Da ebenso wie der Eintrittswinkel wegen der festen Geometrie die Eintrittsquerschnittsfläche unverändert bleibt, ändert sich nach der Kontinuitätsgleichung ![]() die Fördermenge proportional mit der Eintrittsgeschwindigkeit
die Fördermenge proportional mit der Eintrittsgeschwindigkeit ![]() . Es ändert sich
. Es ändert sich ![]() auf
auf ![]() im gleichen Verhältnis wie die Drehzahl, damit ergibt sich für den Volumenstrom
im gleichen Verhältnis wie die Drehzahl, damit ergibt sich für den Volumenstrom
![]()
und damit für den rechnerisch zu ermittelnden Volumenstrom:
![]()
Wegen der aus der Hauptgleichung für Strömungsmaschinen bekannten Proportionalität von Förderhöhe bzw. spezifischer Stutzenarbeit zum Produkt aus Umfangsgeschwindigkeit ![]() und Umfangskomponente
und Umfangskomponente ![]() ergibt sich eine quadratische Abhängigkeit zur Drehzahländerung. Für die spezifische Förderenergie, die Förderhöhe, den Pumpendifferenzdruck und das Pumpendrehmoment gilt:
ergibt sich eine quadratische Abhängigkeit zur Drehzahländerung. Für die spezifische Förderenergie, die Förderhöhe, den Pumpendifferenzdruck und das Pumpendrehmoment gilt:
![]()
Die Pumpennutzleistung ist dem Produkt aus Pumpendifferenzdruck und Volumenstrom proportional, deshalb gilt:
![]()
Zu beachten ist, dass sich die Pumpenantriebsleistung nicht nach den Proportionalitätsgesetzen auf andere Drehzahlen umrechnen lässt, da sich der Wirkungsgrad der Pumpe im Kennfeld ändert.
Die Kavitationskenngrößen lassen sich mit den Proportionalitätsgesetzen nicht herleiten. Aus empirischen Ermittlungen wurde folgende Abhängigkeit von der Drehzahländerung ermittelt (siehe dazu auch Kapitel 5 Kavitation):
![Rendered by QuickLaTeX.com \[\boldsymbol {\frac{NPSH_1}{NPSH_2}=\frac{n_{1}^{1,3...2}}{n_{2}^{1,3...2}}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-a0b9a70329a9ae55419adf3838ade549_l3.png)
Zusammenfassend gelten folgende Proportionalitäten:
![]()
 Mittels der vorher dargestellten Proportionalitätsgesetze für Kreiselpumpen kann bei der Pumpenkennfeldermittlung die Genauigkeit der Messwerte bzw. die Güte der Messung überprüft werden. Dazu wird ein sogenanntes
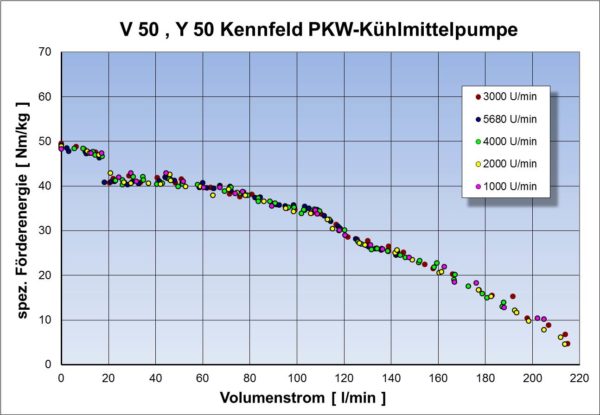
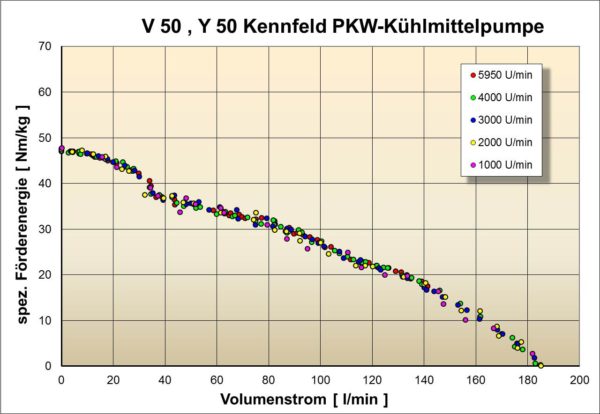
Mittels der vorher dargestellten Proportionalitätsgesetze für Kreiselpumpen kann bei der Pumpenkennfeldermittlung die Genauigkeit der Messwerte bzw. die Güte der Messung überprüft werden. Dazu wird ein sogenanntes ![]() –Kennfeld erstellt (siehe Bilder unten). Die 50 steht dabei für 50 U/s, also für eine Pumpendrehzahl von 3000 U/min. Alternativ kann eine Auftragung über die dimensionslosen Größen Druckzahl und Lieferzahl erfolgen.
–Kennfeld erstellt (siehe Bilder unten). Die 50 steht dabei für 50 U/s, also für eine Pumpendrehzahl von 3000 U/min. Alternativ kann eine Auftragung über die dimensionslosen Größen Druckzahl und Lieferzahl erfolgen.
Es werden die Pumpenkenngrößen bei der Kennfeldermittlung auf die Pumpendrehzahl von 3000 U/min nach den obenstehenden Berechnungsvorschriften umgerechnet. Die Werte müssen dabei etwa auf einer Linie liegen. Ansonsten liegen Fehlmessungen vor oder die Messgenauigkeit z.B. der Druckgeber ist nicht hoch genug. Prinzipiell können auch andere Referenzdrehzahlen als 3000 U/min und andere Pumpenkenngrößen als die spezifische Stutzenarbeit Y gewählt werden.
Zu untersuchen wäre, inwieweit die Proportionalitätsgesetze für Kreiselpumpen auch für nicht voll turbulente Strömung gelten. Dies ist insofern wichtig, als dass bei immer weiter abgesenkter Leerlaufdrehzahl bei Kfz-Verbrennungsmotoren auch die Pumpendrehzahl so weit verringert wird, dass keine voll turbulent ausgebildete Strömung mehr gewährleistet werden kann. Damit ergeben sich wegen des geringeren Wärmeaustausches und des Ansteigens des Strömungswiderstandes Kühlungsprobleme z.B. im Heißleerlauf. Es wird nur noch unzureichend die Wärme von den Zylinderlaufbuchsen sowie im Zylinderkopf abgeführt und es kann zur Motorüberhitzung kommen.
Im ![]() –Kennfeld sollte erkennbar sein, wenn keine hydraulisch raue Strömung mehr vorliegt, indem die Werte der Messung bei dieser kleinen Drehzahl wesentlich von der gemeinsamen Kennlinie abweichen. Im Pumpenkennfeld sind solche Abweichungen nicht zu erkennen, da die kleinste Drehzahl meist achsennah zur X-Achse liegt. Somit kann das
–Kennfeld sollte erkennbar sein, wenn keine hydraulisch raue Strömung mehr vorliegt, indem die Werte der Messung bei dieser kleinen Drehzahl wesentlich von der gemeinsamen Kennlinie abweichen. Im Pumpenkennfeld sind solche Abweichungen nicht zu erkennen, da die kleinste Drehzahl meist achsennah zur X-Achse liegt. Somit kann das ![]() -Kennfeld frühzeitig im Motorentwicklungsprozess auf Kühlungsprobleme hinweisen.
-Kennfeld frühzeitig im Motorentwicklungsprozess auf Kühlungsprobleme hinweisen.
Der Kennlinienverlauf der Kühlmittelpumpe kann mit Variation des Schaufelraddurchmessers, z.B. durch Abdrehen, beeinflusst werden. Mit ![]() als Ausgangsdurchmesser und
als Ausgangsdurchmesser und ![]() als vorgegebenem oder zu berechnendem Durchmesser gilt:
als vorgegebenem oder zu berechnendem Durchmesser gilt:
![]()
![]()
![]()
Unter Voraussetzung gleicher Pumpenwirkungsgrade gilt die Gleichung zur Umrechnung der Pumpennutzleistung auch für die Pumpenantriebsleistung.