1. Berechnung von ![]() über die Einlaufziffer und den volumetrischen Wirkungsgrad
über die Einlaufziffer und den volumetrischen Wirkungsgrad
Der Eintrittsquerschnitt berechnet sich aus:
![]()
Der Eintrittsquerschnitt sollte in Hinblick auf ein gutes Saugverhalten über die nicht zu groß zu wählende Ansauggeschwindigkeit ![]() festgelegt werden:
festgelegt werden:
![]()
Die Einlaufziffer ![]() wird aus der empirischen Formel nach Pfleiderer, C., Petermann, H.: Strömungsmaschinen, 6. Auflage, Springer-Verlag, Berlin 1991 berechnet:
wird aus der empirischen Formel nach Pfleiderer, C., Petermann, H.: Strömungsmaschinen, 6. Auflage, Springer-Verlag, Berlin 1991 berechnet:
![]()
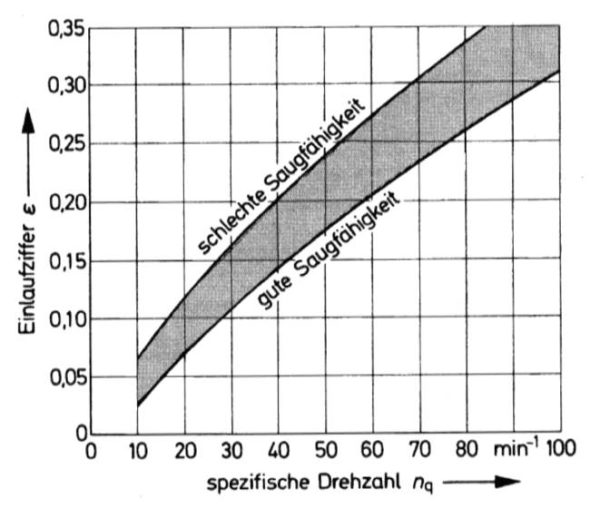
Da der Faktor in obenstehender Gleichung zwischen (1,5…3,0) als großer Bereich erscheint, sollte die Ermittlung der Einlaufziffer nach folgendem Kurvenverlauf gegebenenfalls genauere Ergebnisse liefern:
(Definition von Laufzahl und spezifischer Drehzahl in Kap. 4.2)
Für die Ansauggeschwindigkeit ![]() werden Werte zwischen 2 m/s und 4 m/s empfohlen.
werden Werte zwischen 2 m/s und 4 m/s empfohlen.
Hier sei kurz auf die Geschwindigkeit ![]() hingewiesen. Die Geschwindigkeit
hingewiesen. Die Geschwindigkeit ![]() , die die Strömung kurz vor der Schaufel aufweist, kann gleich der Geschwindigkeit
, die die Strömung kurz vor der Schaufel aufweist, kann gleich der Geschwindigkeit ![]() gesetzt werden. Empfohlen wird jedoch, sie etwas größer zu wählen. Dadurch erreicht man eine kleine Geschwindigkeitssteigerung bis zur Eintrittskante. Diese Beschleunigung verhindert ein Ablösen der Strömung vom stark gekrümmten Einlauf:
gesetzt werden. Empfohlen wird jedoch, sie etwas größer zu wählen. Dadurch erreicht man eine kleine Geschwindigkeitssteigerung bis zur Eintrittskante. Diese Beschleunigung verhindert ein Ablösen der Strömung vom stark gekrümmten Einlauf:
![]()
Der zur Ermittlung des Eintrittsquerschnittes erforderliche Nabendurchmesser wird nach Kap. 4.11.5 berechnet.
Weiterhin wird der volumetrische Wirkungsgrad ![]() benötigt. Er kann aus Erfahrungswerten abgeschätzt oder überschläglich vorausberechnet werden:
benötigt. Er kann aus Erfahrungswerten abgeschätzt oder überschläglich vorausberechnet werden:
![]()
Jetzt sind alle Kenngrößen zur Berechnung des Saugmunddurchmessers ![]() bekannt:
bekannt:
![Rendered by QuickLaTeX.com \[\boldsymbol {D_{S}=\sqrt{\frac{4\cdot \dot{V}}{\pi \cdot \eta_l \cdot c_S}+d_N^2}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-482f38524c777e7ab47460cf6c9ed74a_l3.png)
2. Berechnung von ![]() über
über ![]()
Der Saugmunddurchmesser ![]() kann über den Erfahrungswert
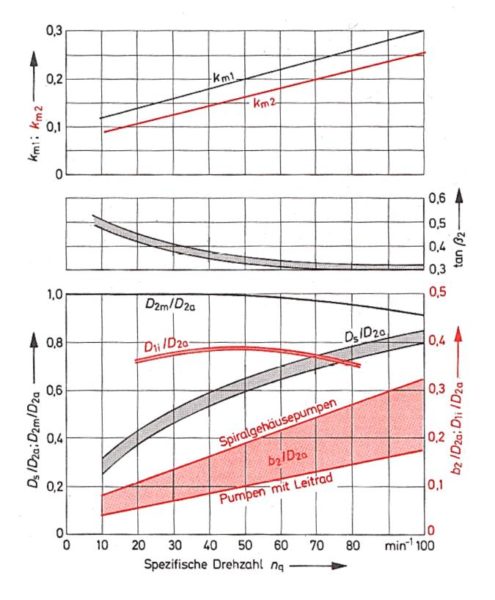
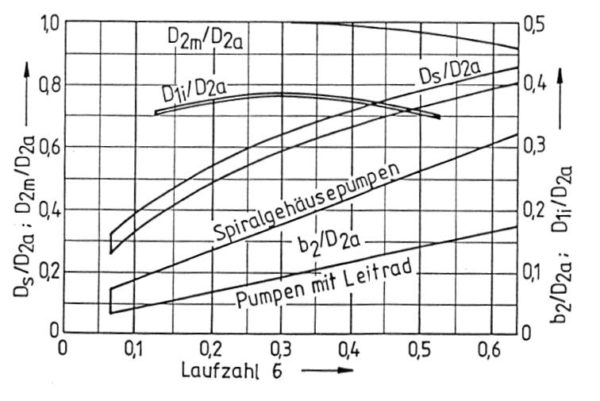
kann über den Erfahrungswert ![]() aus folgendem Kurvenverlauf entnommen werden (Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg), links in Abhängigkeit von der spezifischen Drehzahl und rechts von der Laufzahl :
aus folgendem Kurvenverlauf entnommen werden (Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg), links in Abhängigkeit von der spezifischen Drehzahl und rechts von der Laufzahl :
![]()
Ich bin der Meinung, dass bei bestehenden Schaufelrädern von PKW-Kühlmittelpumpen der Saugmunddurchmesser oft zu groß gewählt wurde und dass man mit einem kleineren Durchmesser Vorteile hinsichtlich Bauraum und Kavitation erreichen könnte. Bei klassischen radialen Schaufelrädern, bei denen der Nabenbereich in die Saugmundebene hineingezogen ist, weil z.B. die dynamische Pumpenabdichtung den Bauraum hinter dem Schaufelrad benötigt oder aus anderen Gründen kein axialer Bauraum vorhanden ist, ist die Nabenversperrung vollständig zu beachten. Jedoch bei einem konstruktiv zurückgezogenen Nabenbereich sollte die Nabe die Einströmung nicht mehr versperren und ein geringerer Saugmunddurchmesser kann möglich sein.