4.11.7 Berechnung der Eintritts- und Austrittsbreite

1. Berechnung der Schaufelrad-Eintrittsbreite b_1

a) Berechnung der Schaufelrad-Eintrittsbreite b_1 mit dem Beiwert k_{m1}

Nach Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg wird der Beiwert k_{m1} ermittelt:

Mittels dieses Beiwertes errechnet sich die Meridiangeschwindigkeit c_{m1} aus:

    \[\boldsymbol {c_{m1}=k_{m1}\cdot \sqrt{2\cdot g \cdot H}}\]

In verschiedenen Literaturquellen wird für Meridiangeschwindigkeit c_{m1} ein Bereich von (1,1…1,3)·c_S empfohlen.

Dann wird der Durchmesser D_{1i} über den Erfahrungswert D_{1i}/D_{2a} ermittelt:

    \[\boldsymbol {D_{1i}=\left(\frac{D_{1i}}{D_{2a}}\right)\cdot D_{2a}}\]

Mit D_{1i} und D_{S} wird D_{1m} ermittelt:

    \[\boldsymbol {D_{1m}=\frac{D_{S}+D_{1i}}{2}}\]

Nun kann die Schaufelradbreite b_{1} berechnet werden:

    \[\boldsymbol {b_{1}=\frac{\dot{V}}{D_{1m}\cdot \pi \cdot c_{m1} }\cdot k_{1}}\]

Der Verengungsfaktor k_1 kann abgeschätzt oder nach folgenden Beziehungen berechnet werden:

Die Eintrittsschaufelteilung t_1 ergibt sich aus

    \[\boldsymbol {t_{1}=\frac{D_1\cdot \pi}{z}}\]

Die Projektion der Schaufeldicke am Schaufelanfang \sigma_1 wird berechnet mit

    \[\boldsymbol {\sigma_1=\frac{s_1}{\sin\beta_1}}.\]

Der Verengungsfaktor k_1 ergibt sich damit aus:

    \[\boldsymbol {k_1=\frac{t_1}{\left(t_1-\sigma_1\right)}}\]

Der Verengungsfaktor k_1 liegt zwischen 1,1 bis 1,3.

b) Berechnung der Schaufelrad-Eintrittsbreite b_1 nach Weber, F.J.: Arbeitsmaschinen: Kreiselpumpen und Verdichter, 2., verbesserte Ausgabe. VEB Verlag Technik Berlin 1962

Sind der Durchmesser D_{1m} und die Ansauggeschwindigkeit c_{S} bekannt, kann mit c_{0}=1…1,1 \cdot c_S die Eintrittsbreite berechnet werden:

    \[\boldsymbol {b_{1}=\frac{\dot{V}_{Rad}}{D_{1m}\cdot \pi \cdot c_{0}}}\]

Bei dieser Formel zeigt sich, dass Weber  im Gegensatz zu Bohl den Radvolumenstrom zur Berechnung heranzieht und nicht den  Auslegungsvolumenstrom. Weber sagt jedoch, dass sich der Schaufelvolumenstrom \dot{V}_{Rad} aus dem Spaltvolumenstrom und der durch Wandreibung verzögerten Strömungsgeschwindigkeit ergibt. Für unsere Kraftfahrzeugpumpen wird jedoch folgende Aussage vorgeschlagen: Der Radvolumenstrom ergibt sich aus dem Auslegungsvolumenstrom zuzüglich Spaltvolumenstrom und Entlastungsbohrungsvolumenstrom. Diese  Volumenstromaufschläge sowie die Aufschläge durch Flüssigkeitsreibung werden prozentual in dem Diagramm nach Kap. 4.11.1 angegeben oder können konkret berechnet oder aus Erfahrungswerten abgeschätzt werden.

Es gilt also:

    \[\boldsymbol {\dot{V}_{Rad}=\dot{V}+\dot{V}_{V}=\dot{V}+\dot{V}_{Sp}+\dot{V}_{EB}}\]

In Verhältnis zum Nutzvolumenstrom \dot{V} wird eine große Spanne von \dot{V}_{Rad}=(1,02…1,15)\cdot \dot{V} angegeben.

Weber gibt an, dass die hier berechnete Eintrittsbreite eine theoretische Kenngröße ist, über die die Strömung am Schaufelradeintritt ungestört verläuft. Bei plötzlicher Richtungsänderung kann jedoch ein Ablösen der Strömung an der Schaufelraddeckscheibe und damit eine Totraumzone entstehen.

Bei kleinem Krümmungsradius am Einlauf gilt für die konstruktive Eintrittsbreite b_{1k}:

    \[\boldsymbol {b_{1k}=\left(1,1...1,25\right)\cdot b_{1}}\]

Mit größerem  Krümmungsradius am Einlauf und steigender Schaufelradbreite wird der Zuschlag zu b_{1} kleiner und geht gegen Null.

formelzeichen 4.11.7

2. Berechnung der Schaufelrad-Austrittsbreite 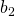b_2

a) Berechnung der Schaufelrad-Austrittsbreite b_2 mit dem Beiwert k_{m2}

Die Berechnung der Schaufelrad-Austrittsbreite erfolgt analog zur Eintrittsbreitenberechung, oben 1a), nach Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg, aber für die Stelle 2 am Schaufelrad:

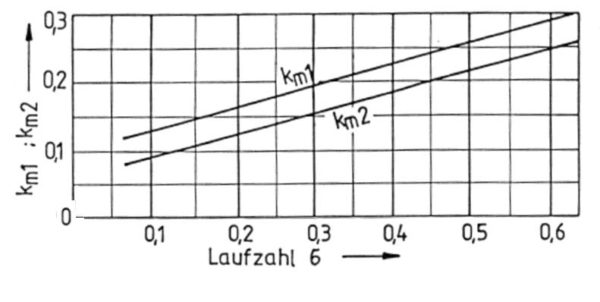
Zunächst wird die Meridiangeschwindigkeit bestimmt. Dazu wird wie schon bei der Eintrittsbreitenberechung aus dem Beiwerte-Diagramm der entsrechende Wert, hier k_{m2}, ermittelt:

Es gilt:

    \[\boldsymbol {c_{m2}=k_{m2}\cdot \sqrt{2\cdot g \cdot H}}\]

Aus dem Diagramm oben rechts  wird der Erfahrungswert D_{2m}/D_{2a} entnommen.

Damit wird:

    \[\boldsymbol {D_{2m}=\left(\frac{D_{2m}}{D_{2a}}\right)\cdot D_{2a}}\]

Nun kann die Schaufelrad-Austrittsbreite b_2 berechnet werden:

 

    \[\boldsymbol {b_{2}=\frac{\dot{V}}{D_{2m}\cdot \pi \cdot c_{m2}}\cdot k_{2}}\]

Der Verengungsfaktor k_2 kann abgeschätzt oder nach folgenden Beziehungen berechnet werden:
Die Austrittsschaufelteilung t_2 ergibt sich aus

    \[\boldsymbol {t_{2}=\frac{D_2\cdot \pi}{z}}.\]

Die Projektion der Schaufeldicke am Schaufelende \sigma_2 wird berechnet mit

    \[\boldsymbol {\sigma_2=\frac{s_2}{\sin\beta_2}}.\]

Der Verengungsfaktor k_2 ergibt sich damit aus:

    \[\boldsymbol {k_2=\frac{t_2}{\left(t_2-\sigma_2\right)}}\]

b) Berechnung von b_2 über den Beiwert b_2/D_{2a}

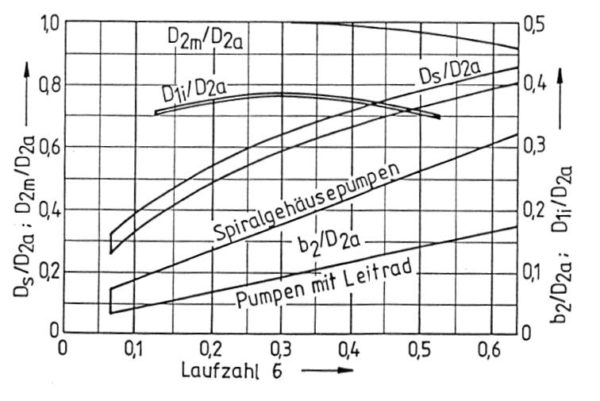
Aus der schon bekannten Grafik aus Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg kann in Abhängigkeit von der Laufzahl der Beiwert b_2/D_{2a} entnommen werden, wobei für uns die Kurve für Spiralgehäusepumpen gilt:

Es gilt bei bekanntem D_{2a}:

    \[\boldsymbol {b_{2}=\left(\frac{b_2}{D_{2a}}\right)\cdot D_{2a}}\]

c) Berechnung der Schaufelrad-Eintrittsbreite b_2 nach Weber, F.J.: Arbeitsmaschinen: Kreiselpumpen und Verdichter, 2., verbesserte Ausgabe. VEB Verlag Technik Berlin 1962

Es gilt:

    \[\boldsymbol {b_{2}=\frac{\dot{V}_{Rad}\cdot \frac{t_{2}}{t_{2}-\sigma_2}}{\pi\cdot D_{2} \cdot c_{m2}}}\]

Die Werte für t_2, \sigma_2 sowie c_{m2} werden wie in  2a) berechnet.

Der nutzbare Durchflussquerschnitt am Schaufelradaustritt und am Eintritt der Leiteinrichtung wird durch eine Sekundärströmung verengt. Die aus dem Schaufelrad mit hoher Geschwindigkeit austretende Strömung kann in der nachgeschalteten Leiteinrichtung stark verzögert werden, wobei es in der Grenzschicht an den Seitenwänden zu einem Rückströmen in das Schaufelrad kommt.

Die Größe dieses Austauschstromes nimmt bei Drosselregulierung mit kleiner werdendem Förderstrom zu und füllt bei Nullförderung die ganze Breite des Schaufelradendes bzw. des Leiteinrichtungseinlaufes aus. Diese Verengung infolge des Austauschverlustes wird durch Vergrößern der oben errechneten Austrittsbreite auf die konstruktive Austrittsbreite b_{2k} berücksichtigt und durch Abschrägen der Seitenwände verringert.

    \[\boldsymbol {b_{2k}=b_{2}+\left(1,0...1,5\right)mm}\]

nächstes Kapitel