1. Allgemeines
Üblicherweise werden für Kfz-Kühlmittelpumpen radiale Kreiselpumpen genutzt. Die Verwendung eines Halbaxialrades oder eines Axialrades kann notwendig werden, wenn wegen einer vorgegebenen Bauraumbeschränkung am Fahrzeugmotor der maximale Schaufelraddurchmesser vorgegeben ist und der notwendige Auslegungspunkt nur durch Drehzahlerhöhung erreicht werden kann. Mit höheren spezifischen Drehzahlen bzw. größerer Schnellläufigkeit ändern sich die Schaufelradformen vom Radialrad über das Halbaxialrad zum Axialrad, siehe auch Kapitel 4.7.
Eine Axialpumpe befördert das Fluid parallel zur Pumpenwelle. Im Gegensatz zur Radialpumpe erfordert das Wirkungsprinzip einer Axialpumpe keine Umlenkung des Förderstromes. Axialpumpen bestehen im Prinzip aus einem rohrförmigen Pumpengehäuse, in dem ein propellerähnliches Schaufelrad rotiert. Der Antrieb erfolgt meistens durch eine vom Fördermedium umströmte Antriebswelle, an welcher sich eine Antriebsscheibe oder ggf. ein Motor oder Getriebe befindet. Es ist auch möglich, eine Axialpumpe von außen rein magnetisch anzutreiben. Hierzu kann auf den Pumpenschaufeln ein ringförmiger Drehstrommotor – Kurzschlussläufer angebracht werden. Um das rohrförmige Pumpengehäuse befindet sich der Stator des Motors. Mit solch einer Läufer-Stator-Anordnung ist der Motor hermetisch dicht.
Die Auslegung der Halbaxialräder erfolgt im Prinzip wie bei den Radialrädern. Bei größer werdenden spezifischen Drehzahlen sind jedoch immer abweichendere Besonderheiten wie z.B. die aerodynamische bzw. strömungstechnische Auslegung der Tragflügelprofile notwendig. Die Darlegung der physikalischen, mathematischen und geometrischen Auslegungsvorschriften weist eine hohe Komplexität auf und wird nachfolgend einleitend behandelt. Die Ausführungen dazu sind den Fachbüchern Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg und Weber, F.J.: Arbeitsmaschinen: Kreiselpumpen und Verdichter, 2., verbesserte Ausgabe. VEB Verlag Technik Berlin 1962 entnommen. Diese zwei alternativen Auslegungsmethoden können auch verwendet werden, um für unsere kleinen PKW-Axialpumpen eine optimale Schaufelradgestaltung zu finden.
Ausführlichere Beschreibungen zur Axialpumpenberechnung können der vertiefenden Auslegungssystematik nach Members of the staff of Lewis Research Center: Aerodynamic Design of Axial-Flow-Compressors. NASA SP-36, Washington D.C., 1965 entnommen werden.
Zu beachten ist, dass die in Bohl/Elmendorf und Weber enthaltenen Berechnungsvorschriften und dazugehörigen Grafiken für größere axiale Schaufelraddurchmesser erstellt wurden und deswegen bei unseren kleinen PKW-Pumpenraddurchmessern Abweichungen und damit (wahrscheinlich erhebliche) Berechnungskorrekturen zu erwarten sind.
Das beschaufelte Leitrad hat die Aufgabe, die aus dem Schaufelrad austretende Strömung stoßfrei weiterzuleiten und die Geschwindigkeitsenergie in Druckenergie umzuwandeln. Nach Weber haben Leiträder (auch beschaufelte Leitkränze genannt) entweder parallele oder leicht schräge Seitenwände und vom Schaufelrad abweichende Schaufelzahlen, damit periodische Schwingungen verhindert werden, wobei auch ein ganzzahlig Vielfaches zu vermeiden ist.
Es besteht die Möglichkeit, das Leitrad dem Schaufelrad vor- oder nachzuschalten oder sogar zwei Leiträder zu verwenden, indem jeweils an der Druckseite und an der Saugseite ein Leitrad installiert wird. Bei der Verwendung von Eintrittsleiträdern ist darauf zu achten, dass keine Drucksenkung durch Beschleunigung der Strömung auftritt, da damit die Kavitationsgefahr erhöht wird.
Zur Auslegung von bewegten Axialgittern (Schaufelräder) und stehenden Axialgittern (Leiträder) können die entsprechenden Vorschriften aus den oben aufgeführten sowie darin weiteren genannten Literaturstellen herangezogen werden.
2. Berechnung der Axialrad-Hauptabmessungen nach Weber, F.J.: Arbeitsmaschinen: Kreiselpumpen und Verdichter, 2., verbesserte Ausgabe. VEB Verlag Technik Berlin 1962
Bei Axialpumpen mit zylindrischer Gehäusebegrenzung und zylindrischer Nabe zeigt das Strömungsbild achsparallele Flusslinien.
Die Theoretische Hauptgleichung für Strömungsmaschinen gilt für Axialpumpen und unendlicher Schaufelzahl in der Form
![]()
und für endliche Schaufelzahl in der Form
![]()
Die Indizes 0 bezeichnen einen Punkt kurz vor dem Schaufelrad und 3 kurz nach dem Schaufelrad. In obenstehenden Gleichungen ist u = r ![]() die Umfangsgeschwindigkeit des jeweils betrachteten Zylinderschnittes im Abstand r. Gleiches gilt für die
die Umfangsgeschwindigkeit des jeweils betrachteten Zylinderschnittes im Abstand r. Gleiches gilt für die ![]() -Komponenten.
-Komponenten.
Zur Festlegung der Schaufelzahl z gilt
![]()
mit e Länge der mittleren Flusslinie, ![]() Schwerpunkthalbmesser der mittleren Flusslinie und
Schwerpunkthalbmesser der mittleren Flusslinie und ![]() Erfahrungszahl für die Schaufelgüte (Schaufeldicke, Oberflächenbeschaffenheit, Herstellungsgenauigkeit).
Erfahrungszahl für die Schaufelgüte (Schaufeldicke, Oberflächenbeschaffenheit, Herstellungsgenauigkeit).
Die Gleichung zur Schaufelzahlfestlegung kann nur angewendet werden, wenn die Projektionslänge e der Schaufel im Meridianschnitt in Höhe des mittleren Stromfadens und die Winkel ![]() und
und ![]() an der gleichen Stelle bekannt sind, was allerdings erst nach endgültiger Auslegung des Tragflügelprofils möglich ist. Die Gleichung wird also erst zur Nachrechnung verwendet.
an der gleichen Stelle bekannt sind, was allerdings erst nach endgültiger Auslegung des Tragflügelprofils möglich ist. Die Gleichung wird also erst zur Nachrechnung verwendet.
Für den ersten Entwurf der Schaufelzahl kann angewendet werden:
z = 7…4 bei ![]() = 100…200
= 100…200
z = 4…3 bei ![]() = 200…300
= 200…300
z = 3…2 bei ![]() > 300
> 300
Das Verhältnis der statischen Druckhöhe zur Gesamtförderhöhe ist der Reaktionsgrad des Schaufelrades. Für Axialräder errechnet sich der Reaktionsgrad aus
![]()
Der Reaktionsgrad kann bei Axialmaschinen nicht nur Werte zwischen 0 und 1 annehmen. Er wird nach obenstehender Gleichung bei ![]() > 0, d.h. bei
> 0, d.h. bei ![]() » 90°, größer als 1. Damit wird ein Eintrittsleitrad für den Gegendrall notwendig.
» 90°, größer als 1. Damit wird ein Eintrittsleitrad für den Gegendrall notwendig.
Der Außenradius ![]() des axialen Schaufelrades ergibt sich aus der Umstellung der Durchflussgleichung für den Kreisringquerschnitt kurz vor Schaufelbeginn aus:
des axialen Schaufelrades ergibt sich aus der Umstellung der Durchflussgleichung für den Kreisringquerschnitt kurz vor Schaufelbeginn aus:
![Rendered by QuickLaTeX.com \[\boldsymbol {r_a=\sqrt[3]{\frac{\dot{V}}{\pi \cdot k_n \cdot \delta_r \cdot \omega \cdot tan\beta_{a0}}}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-217c0664c899d887fe2d145078ddb84b_l3.png)
Für die Verengungszahl ![]() gilt:
gilt:
![]()
Für die relative Drallzahl ![]() gilt:
gilt:
![]()
Für den relativen Strömungswinkel am Außenrand kurz vor Beginn der Schaufel ![]() gelten Optimalwerte, die nicht überschritten werden sollen. Für Wasserförderung beträgt dieser Optimalwert bei Drallfreiheit unter Berücksichtigung der Kavitation
gelten Optimalwerte, die nicht überschritten werden sollen. Für Wasserförderung beträgt dieser Optimalwert bei Drallfreiheit unter Berücksichtigung der Kavitation ![]() = 17…18°. Ist keine Drallfreiheit vorhanden, vergrößert sich dieser Wert etwas.
= 17…18°. Ist keine Drallfreiheit vorhanden, vergrößert sich dieser Wert etwas.
Das Nabenverhältnis ![]() bzw. der reziproke Wert
bzw. der reziproke Wert ![]() kann aus entsprechenden Kennlinienverläufen in Weber, F.J.: Arbeitsmaschinen: Kreiselpumpen und Verdichter, 2., verbesserte Ausgabe. VEB Verlag Technik Berlin 1962 entnommen werden.
kann aus entsprechenden Kennlinienverläufen in Weber, F.J.: Arbeitsmaschinen: Kreiselpumpen und Verdichter, 2., verbesserte Ausgabe. VEB Verlag Technik Berlin 1962 entnommen werden.
Die Einlaufzahl ε errechnet sich aus (mit ![]() in
in ![]() ):
):
![]()
3. Berechnung der Axialrad-Hauptabmessungen nach Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg
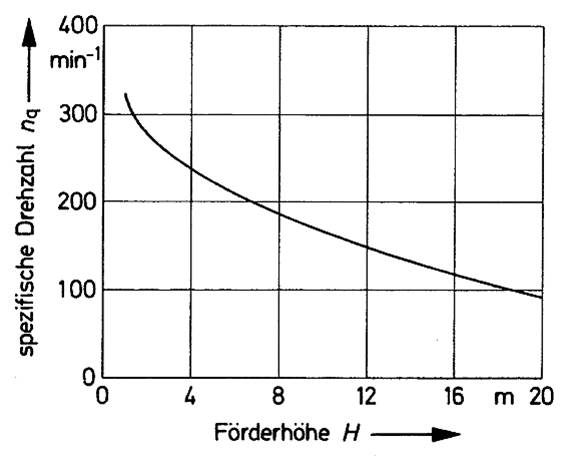
Ist zur Axialradauslegung der Auslegungspunkt mit dem Volumenstrom ![]() und der Förderhöhe H oder der spezifischen Stutzenarbeit Y vorgegeben, kann die optimale spezifische Drehzahl
und der Förderhöhe H oder der spezifischen Stutzenarbeit Y vorgegeben, kann die optimale spezifische Drehzahl ![]() aus folgender Grafik entnommen werden, wobei für kleine PKW-Axialpumpen der ganz linke Bereich der Kennlinie gilt:
aus folgender Grafik entnommen werden, wobei für kleine PKW-Axialpumpen der ganz linke Bereich der Kennlinie gilt:
Der Außendurchmesser von Axialpumpenschaufelrädern kann (ähnlich wie in Kapitel 4.11.3 bereits für radiale Schaufelräder dargestellt) über die Druckzahl ![]() , welche ihrerseits von der spezifischen Drehzahl
, welche ihrerseits von der spezifischen Drehzahl ![]() abhängt, ermittelt werden:
abhängt, ermittelt werden:
![Rendered by QuickLaTeX.com \[\boldsymbol {D_a=0,45 \cdot \frac{1}{n}\cdot \sqrt{\frac{Y}{\psi}}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-130955a482585745ea31922bbd15a022_l3.png)
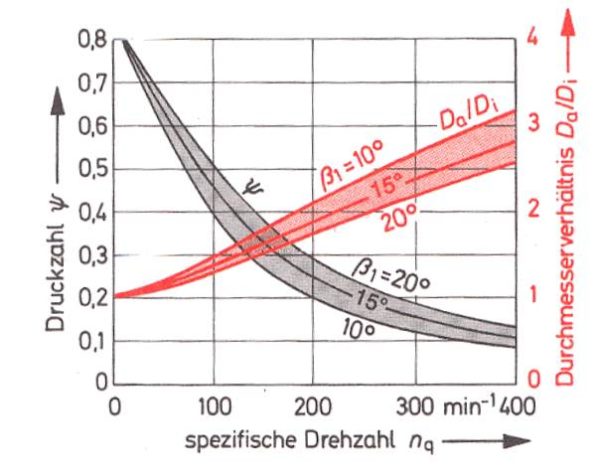
Die Druckzahl ![]() kann ebenso wie weitere Axialradkennwerte aus untenstehender Grafik entnommen werden:
kann ebenso wie weitere Axialradkennwerte aus untenstehender Grafik entnommen werden:
Eine Kontrolle des ermittelten Außendurchmessers erfolgt über seine Berechnung mit dem Beiwert der Umfangsgeschwindigkeit ![]() :
:
![]()
Der Beiwert ![]() kann aus untenstehender Grafik entnommen oder folgender empirischer Formel abgeschätzt werden:
kann aus untenstehender Grafik entnommen oder folgender empirischer Formel abgeschätzt werden:
![]()
Zur Bestimmung des Nabenverhältnisses ![]() werden in Bohl/Elmendorf mehrere Verfahren angegeben. Zunächst kann aus der weiter oben gezeigten Grafik Auslegewerte für axiale Pumpenschaufelräder das Durchmesserverhältnis
werden in Bohl/Elmendorf mehrere Verfahren angegeben. Zunächst kann aus der weiter oben gezeigten Grafik Auslegewerte für axiale Pumpenschaufelräder das Durchmesserverhältnis ![]() in Abhängigkeit von der spezifischen Drehzahl
in Abhängigkeit von der spezifischen Drehzahl ![]() ermittelt werden.
ermittelt werden.
Weiterhin kann der Innendurchmesser ![]() über die mittlere Meridiangeschwindigkeit berechnet bzw. kontrolliert werden, wobei folgende Beziehungen gelten:
über die mittlere Meridiangeschwindigkeit berechnet bzw. kontrolliert werden, wobei folgende Beziehungen gelten:
![Rendered by QuickLaTeX.com \[\boldsymbol {c_m\approx \frac{\dot V}{\frac{\pi}{4}\cdot \left(D_a^2-D_i^2\right)}=k_{cm}\cdot \sqrt{2 \cdot Y}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-4e301ef82c094c1a6f5072500dc015e3_l3.png)
![Rendered by QuickLaTeX.com \[\boldsymbol {D_i=\sqrt{D_a^2-\frac{4 \cdot \dot V}{\pi \cdot k_{cm}\cdot \sqrt{2 \cdot Y}}}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-5eeafae30db3fd6aa9381dd9124ddc02_l3.png)
Die Meridiangeschwindigkeit sollte innerhalb des Bereiches
![]()
liegen, mit n in ![]() .
.
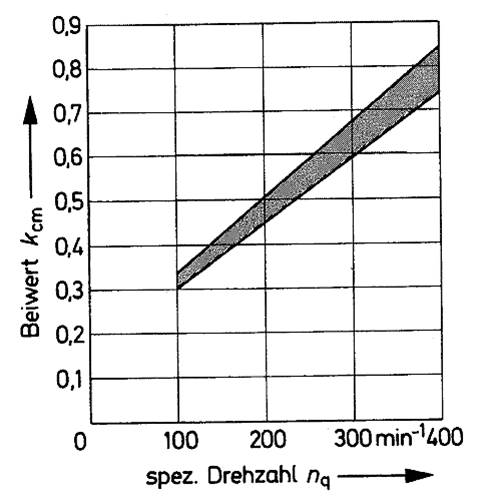
Der Beiwert der Meridiangeschwindigkeit ![]() kann empirisch aus
kann empirisch aus
![]()
berechnet oder aus folgender Grafik entnommen werden:
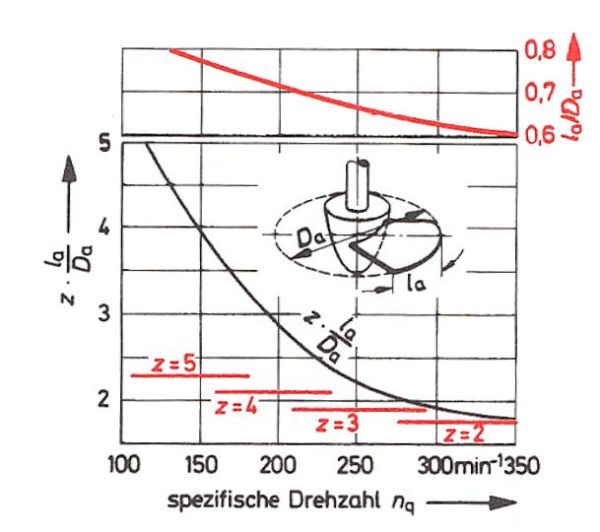
Die Schaufelzahl z liegt i.A. zwischen 3 und 6. Sie kann mit untenstehender Grafik aus dem Verhältnis von ![]() in Funktion von
in Funktion von ![]() ermittelt werden. In dieser Grafik sind außerdem Schaufelzahlbereiche vorgeschlagen:
ermittelt werden. In dieser Grafik sind außerdem Schaufelzahlbereiche vorgeschlagen:
Eine genauere Durchrechnung des Schaufelgitters und die endgültige Gestaltung kann den entsprechenden Ausführungen in Bohl/Elmendorf entnommen werden.