Mit den unter Kapitel 5.5 vorgestellten Berechnungsverfahren ergeben sich nur grobe Abschätzungen der Kavitationskennwerte im Optimalpunkt. Bei bekannten, z.B. messtechnisch ermittelten (siehe nachfolgende Abschnitte), Kavitationskennwerten kann eine Umrechnung auf andere Betriebszustände bzw. Betriebspunkte oder ggf. auch auf andere Radgeometrien notwendig werden. Ein allgemein gültiges Modellgesetz für solche Umrechnungen ist nicht bekannt. Es wird eingeschätzt, dass auch die Umrechnung der Kavitationswerte nur grob aus empirischen Erfahrungen möglich ist und für genauere Ergebnisse Messungen für die angesprochenen abweichenden Betriebspunkte und Geometrien durchgeführt werden müssen. Da dies in der Vorausauslegung nicht möglich ist und zum Teil da schon Aussagen über das Kavitationsverhalten auch über einen weiten Betriebsbereich notwendig sind, sollen hier Umrechnungsmöglichkeiten aufgezählt werden.
Für den Einfluss auf unterschiedliche Drehzahlen der gleichen Pumpe kann allgemein gesetzt werden mit:
![\[\boldsymbol {\frac{NPSH_{R\,1}}{NPSH_{R\,2}}=\left(\frac{n_1}{n_2}\right)^x}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-baa5226ef5c692f1c4de1d402cd87093_l3.png "Rendered by QuickLaTeX.com")
Der unpräzise Exponent wird in der Literatur mit unterschiedlichen Werten angegeben. Im Kapitel 4.6 Proportionalitätsgesetze wurde bereits darauf hingewiesen, dass die Kavitationskenngrößen sich mit Proportionalitätsgesetzen nicht herleiten lassen. Aus empirischen Ermittlungen wurde folgende Abhängigkeit von der Drehzahländerung ermittelt:
![\[\boldsymbol {\frac{NPSH_{R\,1}}{NPSH_{R\,2}}=\frac{n_1^{1,3...2}}{n_2^{1,3...2}}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-1067e8ee5ec1cc91ab36751dd9ce38c4_l3.png "Rendered by QuickLaTeX.com")
In Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg werden folgende Werte für den Exponenten x mit unterschiedlichen Quellen und Literaturstellen angegeben:
a) 1,5 < x < 1,7
b) 1,3 < x < 2,0
c) x ≈ 2
d) x = 1,5
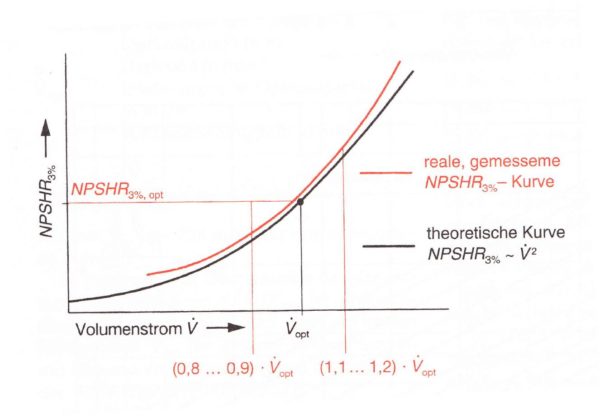
Der Verlauf des Pumpenkavitationswertes im Kurvenverlauf für gleiche Drehzahl und unterschiedliche Volumenströme, also im Teil- und im Überlastbereich, kann nach Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg für Radialpumpen mit niedrigen spezifischen Drehzahlen im Bereich
![\[\boldsymbol {\left(0,8...0,9\right)\cdot \dot{V}_{opt}<\dot{V}_{opt}< \left(1,1...1,2\right)\cdot \dot{V}_{opt}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-d9cdec9101db79b10e837719ca167d82_l3.png "Rendered by QuickLaTeX.com")
annähernd quadratisch angenommen werden:
![\[\boldsymbol {NPSH_{3 \%}\approx NPSH_{3 \%\,opt}\cdot \left(\frac{\dot{V} }{\dot{V}_{opt}}\right)^2}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-6d0cf9b227a306847e97fe8cbdac10ca_l3.png "Rendered by QuickLaTeX.com")
In Versuchen wurde diese quadratische Abhängigkeit bestätigt:
