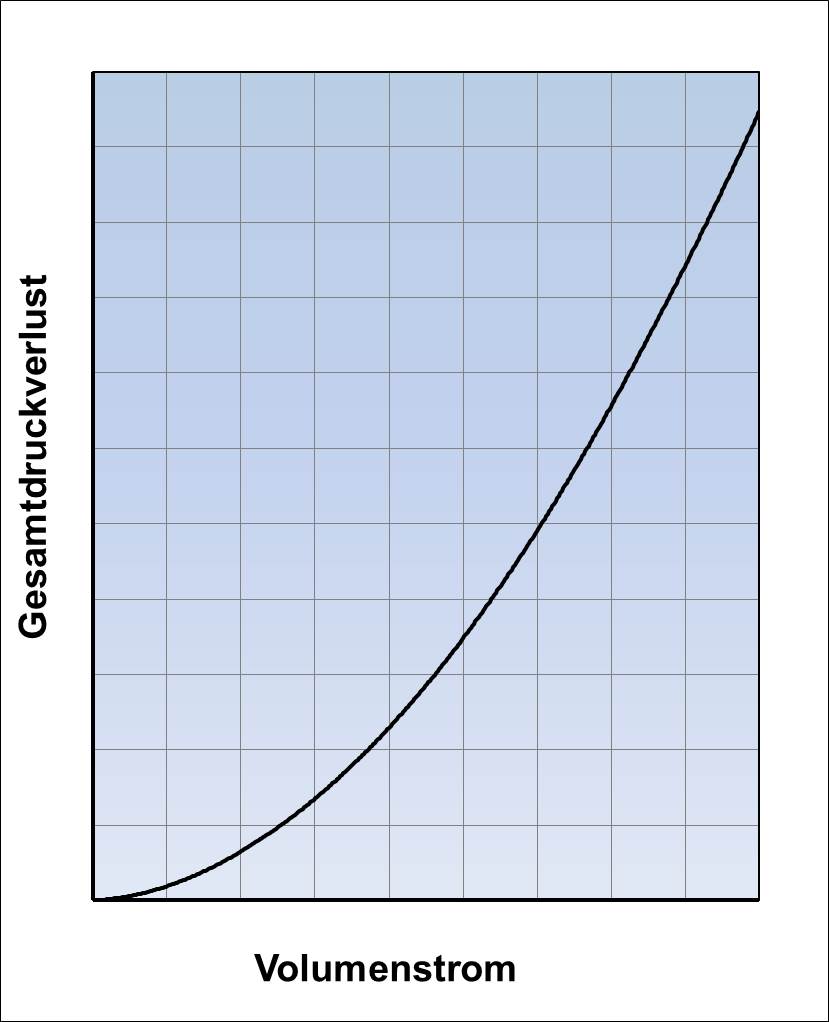
Der Druckverlust eines Kühlkreislaufbauteils kann in Abhängigkeit vom durchgesetzten Volumenstrom dargestellt werden, Bild links (zum Vergrößern anklicken, zurück mit dem Navigationspfeil des Browsers):
Bei unterschiedlichen Strömungsmitteltemperaturen und -zusammensetzungen ergeben sich allerdings auch unterschiedliche Kurvenverläufe. Im rechten Bild ist der Abfall des Gesamtdruckverlustes nach Bernoulli bei steigender Temperatur dargestellt. Der Nachteil dieser Druckverlustdarstellung ist also, dass sie nur für die während der Prüfstandsuntersuchung vorhandene Strömungsmitteltemperatur und -zusammensetzung gültig ist.
Für eine temperatur- und zusammensetzungsunabhängige Darstellung zumindest bei voll ausgebildeter rauer Strömung wird der spezifische Energieverlust eingeführt:
![]()
Der spezifische Energieverlust, der beim Durchströmen eines Bauteils eintritt, ist gleichzeitig eine Funktion des Volumenstromes, dessen Abhängigkeit wie folgt dargestellt werden kann:
![]()
Der Proportionalitätsfaktor R wird als Strömungswiderstand bezeichnet. Er kann für Kühlkreislaufbauteile mit dem Prüfstandsaufbau im nächsten Bild volumenstromabhängig mit
![Rendered by QuickLaTeX.com \[\boldsymbol {R=\frac{Y_{V}}{\dot{V}^2}=\frac{\frac{\left(p_{1}-p_{2}\right)}{\varrho}+g \Delta h+\frac{c_1^2}{2}-\frac{c_2^2}{2}}{\dot{V}^2}=\frac{\Delta p_{ges}}{\varrho\cdot \dot{V}^2}=\frac{\zeta}{2A^{2}}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-bd2485a78292d7af3d635b218478343c_l3.png)
ermittelt werden.

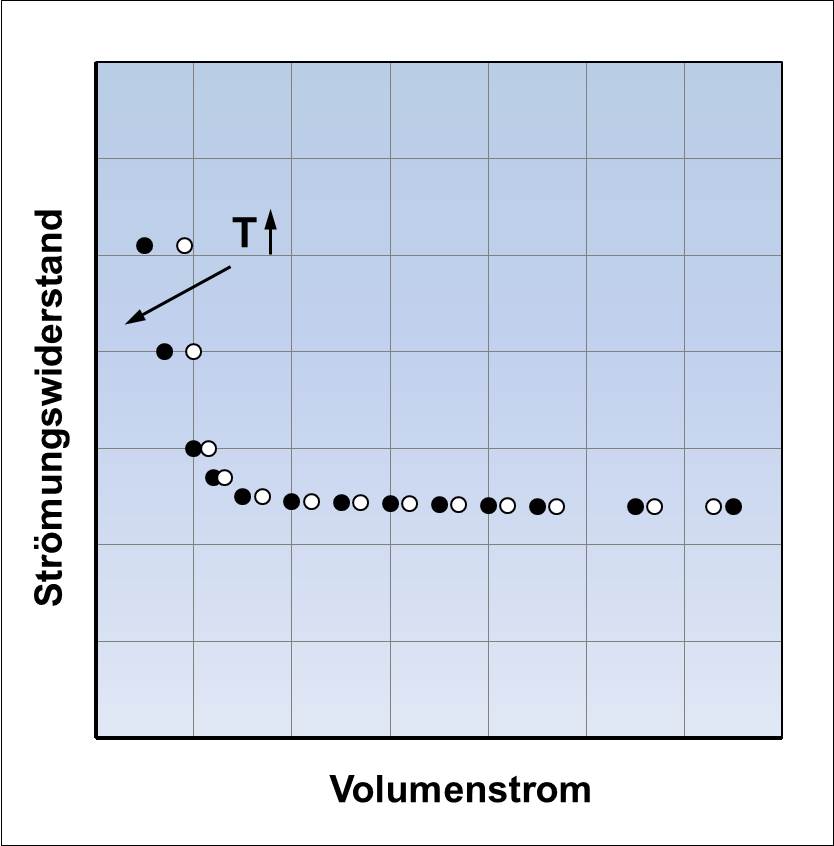
Der typische Verlauf des Strömungswiderstandes eines Kühlkreislaufbauteils wird in folgendem Bild unten links dargestellt:
Der Verlauf des Strömungswiderstandes zeigt deutlich seinen Anstieg bei kleinen Volumenströmen im nicht voll turbulenten Strömungsbereich. In diesem Strömungsbereich ändert sich der Kurvenverlauf bei unterschiedlichen Strömungsmitteltemperaturen (mittleres Bild).
Um auch bei nicht voll ausgebildeter hydraulisch rauer Strömung einen für alle Strömungsmitteltemperaturen und -zusammensetzungen gültigen Kurvenverlauf zu erhalten, wird der Strömungswiderstand in Abhängigkeit vom Quotienten aus Volumenstrom und der kinematischen Zähigkeit des Strömungsmittels dargestellt (Bild rechts).
Üblich ist auch die Darstellung des Druckverlustbeiwertes Zeta in Abhängigkeit von der Reynoldszahl. Vorteil dieser Darstellungsform sind die dimensionslosen Kennwerte, nachteilig ist die bei Kühlkreislaufbauteilen oft unpräzise Definition der Strömungsquerschnitte zur Berechnung der Kenngrößen Zeta und Reynoldszahl, z.B. bei unterschiedlichen Querschnitten vor, im und nach dem Bauteil. Zur Rückrechnung von Druckverlustbeiwert und Reynoldszahl in Druck und Volumenstrom für den zu betrachtenden Kreislaufzustand (Temperatur und Zusammensetzung des Fluids) ist zwingend die Kenntnis des bei der Berechnung von Zeta und Re verwendeten Strömungsquerschnittes notwendig, ansonsten werden die berechneten Werte falsch!
Der Strömungswiderstandbeiwert Zeta ζ berechnet sich aus
![]()
und die Reynoldzahl Re mit
![]()
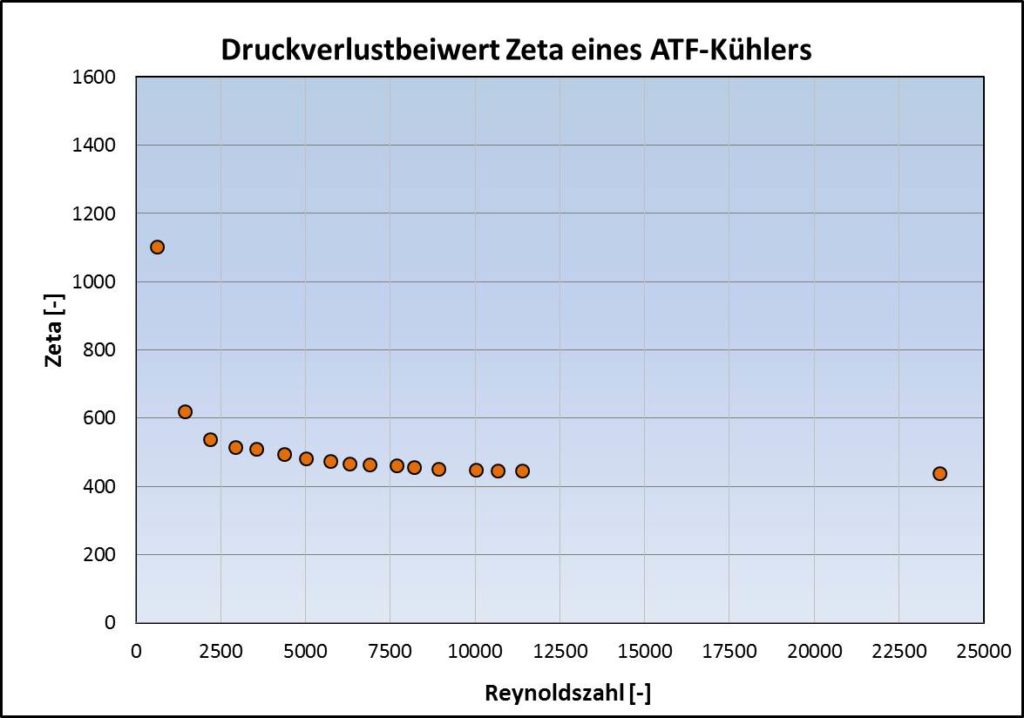
Das Bild unten links zeigt einen mit der prüfstandsermittelten Druckverlustkurve berechneten Druckverlustbeiwert Zeta in Abhängigkeit von der Reynoldszahl eines Motorölkühlers. Gut zu sehen sind die enger abgestuften Meßwerte im Übergangsbereich zu vollständig turbulenter Strömung. Die genaue Druckverlust- bzw. Druckverlustbeiwertermittlung in diesem Reynoldzahlbereich ist notwendig, um exakte Strömungswerte bei kleinen Volumenströmen, z.B. bei niedrigen Motordrehzahlen oder Motorleerlauf, zu erhalten und diese strömungstechnischen und ggf. thermischen Verhältnisse bereits in der Motorauslegungsphase mit hoher Genauigkeit vorauszuberechnen. In Bild rechts ist der Druckverlustbeiwerteverlauf eines ATF-Wärmetauscher aufgezeichnet:
Zu sehen ist, dass sich die Kurvenverläufe der Kühlkreislauf-Druckverlustbeiwerte im Bereich der turbulenten Strömung unterscheiden können. Der Ölkühler weist einen stetig abfallenden Druckverlustbeiwert auf ähnlich dem Rohrreibungsbeiwert bei hydraulisch glatter Strömung im Moody-Diagramm, siehe hier im Kapitel 1.3. Der ATF-Kühler hingegen hat einen ungefähr waagerechten Verlauf bei größeren Reynoldszahlen wie der Rohrreibungsbeiwert bei hydraulisch rauer Strömung. Diese Kurvenverläufe zeigen, dass eine Angabe des Druckverlustes bzw. des Druckverlustbeiwertes nur für einen Volumenstrom oder einer Reynoldszahl zu ungenauen Ergebnissen z.B. bei einer Kreislaufberechnung führt, da über den Reynoldszahlbereich der Druckverlustbeiwert ständig korrigiert werden muss.
Weitere Kennwerte:
Hydraulischer Durchmesser: Bei einem anderen als kreisrunden Stömungsquerschnitt kann der Durchmesser mittels des hydraulischen Durchmessers, manchmal auch Äquivalenzdurchmesser genannt, berechnet werden:
![]()
Für enge Spalte ist die Anwendung dieser Formel allerdings nicht geeignet.
Kinematische und dynamische Viskosität/Zähigkeit: Kinematische und dynamische Viskosität stehen über die Dichte in physikalischem Zusammenhang:
![]()