Der Schaufelradaußendurchmesser ist eine geometrische Schaufelradkenngröße, mit welcher die erreichbare Pumpenförderhöhe wesentlich bestimmt wird. Es ist eine Vielzahl von Berechnungsmethoden zur Ermittlung des Außendurchmessers bekannt. Dabei treten unterschiedlich große Abweichungen zum letztendlich vorhandenen bzw. notwendigen Außendurchmesser auf.
Nachfolgend sollen einige Berechnungsvarianten vorgestellt werden, die teils gute Übereinstimmungen mit den notwendigen Schaufelradaußendurchmessern ergaben. Dabei ist es durchaus möglich, dass für verschiedene Kfz-Kühlmittelpumpen auch unterschiedliche Berechnungsvarianten angewandt werden müssen, d.h. dass es für alle Pumpenausführungen die eine gültige Berechnungsvorschrift nicht gibt. Dies liegt an der empirischen Ermittlung der jeweiligen Auslegungsvorschrift.
Vorgeschlagen wird die Berechnung des Außendurchmessers mit unterschiedlichen Auslegungsvorschriften und der abschließende Vergleich mit dem letztendlich zur Erreichung des geforderten Pumpenauslegungspunktes notwendigen Außendurchmessers. Bei mehreren ausgelegten Pumpen erhält man dann für den jeweiligen Auslegungsfall die Berechnungsvorschrift mit der besten Übereinstimmung.
1. Ermittlung von ![]() über die Druckzahl
über die Druckzahl ![]()
Für die Ermittlung der Druckzahl ![]() werden verschiedene Wege aufgezeigt:
werden verschiedene Wege aufgezeigt:
a) In Schulz, H.: Die Pumpen, 13 Auflage Springer Verlag 1977 werden folgende Richtwerte für die Druckzahl ![]() empfohlen:
empfohlen:
Pumpen mit Spiralgehäuse Druckzahl ![]() = 0,9…1,0
= 0,9…1,0
Pumpen mit Leitrad Druckzahl ![]() = 1,0…1,1
= 1,0…1,1
Pumpen mit Leitring Druckzahl ![]() = 0,8…0.9
= 0,8…0.9
b) Die Druckzahl ![]() kann nach Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg abhängig von der Laufzahl
kann nach Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg abhängig von der Laufzahl ![]() aus folgender Grafik entnommen werden (der ebenfalls dargestellte Geschwindigkeitsbeiwert soll hier zunächst ausgeblendet werden):
aus folgender Grafik entnommen werden (der ebenfalls dargestellte Geschwindigkeitsbeiwert soll hier zunächst ausgeblendet werden):
c) In Pekrun,M.: Wirkungsgrade und Verlustzahlen bei Kreiselpumpen. Vortragsveröffentlichung, Heft 157. Haus der Technik, Essen. Vulkanverlag werden folgende Näherungsgleichungen für ![]() angegeben:
angegeben:
für Laufzahl ![]() = 0,09…0,38
= 0,09…0,38
![]()
für Laufzahl ![]() > 0,38
> 0,38
![]()
Diese Näherungsgleichungen sollten ggf. an moderne, ausgeführte Pumpenschaufelräder anpasst werden.
Nachdem aus den unter a),b) und c) angegebenen Vorschriften die Druckzahl ![]() ermittelt wurde, kann mit folgender Formel der Schaufelradaußendurchmesser
ermittelt wurde, kann mit folgender Formel der Schaufelradaußendurchmesser ![]() berechnet werden:
berechnet werden:
![Rendered by QuickLaTeX.com \[\boldsymbol {D_{2a}=0,45\cdot \frac{1}{n}\cdot\sqrt{\frac{g \cdot H}{\psi}}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-d79a4e930df001101be026ce1ca065f3_l3.png)
2. Ermittlung von ![]() über den Geschwindigkeitsbeiwert
über den Geschwindigkeitsbeiwert ![]()
Der Geschwindigkeitsbeiwert ![]() wird abhängig von der Laufzahl
wird abhängig von der Laufzahl ![]() aus dem unter 1b) (siehe oben) gezeigten Diagramm zur Ermittlung der Beiwerte
aus dem unter 1b) (siehe oben) gezeigten Diagramm zur Ermittlung der Beiwerte ![]() und
und ![]() entnommen. Mit diesem Beiwert ergibt sich eine Umfangsgeschwindigkeit
entnommen. Mit diesem Beiwert ergibt sich eine Umfangsgeschwindigkeit ![]() am Außendurchmesser:
am Außendurchmesser:
![]()
Für die Förderhöhe H sollte ein korrigierter Wert nach 4.11.2 verwendet werden.
Nun kann der Schaufelrad-Außendurchmesser ![]() berechnet werden:
berechnet werden:
![]()
Bei Nachrechnungen ergaben sich mit dieser Methode gute Übereinstimmungen für kleine ausgeführte Schaufelrad-Durchmesser, insofern zur Berechnung ein korrigierter Wert für die Förderhöhe H verwendet wurde.
3. Ermittlung von ![]() nach GRABOW
nach GRABOW
Nach Grabow,G.: Ermittlung der hydraulischen Abmessungen der Laufräder für Kreiselpumpen und Kreiselvedichter. Zeitschrift Konstruktion, 13.Jg (1961) wird der Schaufelrad-Durchmesser mit folgender empirischer Formel entwickelt:
![Rendered by QuickLaTeX.com \[\boldsymbol {D_{2a}=\left(\frac{1,1835\cdot s^{-1}\cdot m^{0,5}+K}{n}\cdot\sqrt{H}\right)}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-3047be032e044547cd4afa70c3d0acfb_l3.png)
mit K=1,1833…1,25 ![]()
4. Ermittlung von ![]() über die Durchmesserzahl
über die Durchmesserzahl ![]()
Die Durchmesserzahl kann nach Berechnung der Laufzahl näherungsweise aus
![]()
errechnet oder aus dem Cordier-Diagramm entnommen werden:
Der Schaufelrad-Durchmesser errechnet sich dann aus:
![Rendered by QuickLaTeX.com \[\boldsymbol {D_{2a}=\delta \cdot\frac{2\cdot \sqrt{\dot V}}{\left(2\cdot g \cdot H\right)^{0,25}\cdot \sqrt{\pi}}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-c492561b2c1c7ee140bd009fa859308e_l3.png)
5. Ermittlung von ![]() nach Weigend, F.: Vergleich von theoretisch und experimentell ermittelten Kühlmittelpumpenkenngrößen, Zwickau: Diplomarbeit Technische Hochschule Zwickau:
nach Weigend, F.: Vergleich von theoretisch und experimentell ermittelten Kühlmittelpumpenkenngrößen, Zwickau: Diplomarbeit Technische Hochschule Zwickau:
F. Weigend gibt folgende empirische Formel zur Berechnung des Schaufelrad-Außendurchmessers an:
![Rendered by QuickLaTeX.com \[\boldsymbol {D_{2a}\approx \sqrt{\frac{g\cdot H}{\eta_{ges}\cdot \mu \cdot \pi^{2}\cdot n^{2}}}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-049d558156cb48c0cca76cc22484ddd9_l3.png)
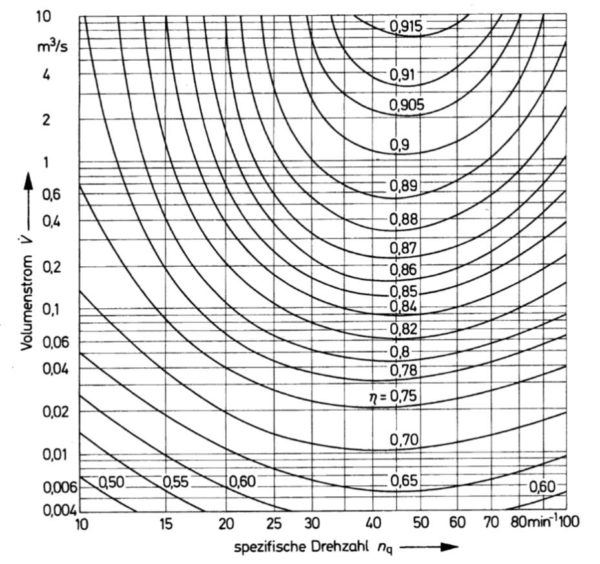
Der Pumpenwirkungsgrad ![]() kann zunächst aus folgender Grafik abgeschätzt werden:
kann zunächst aus folgender Grafik abgeschätzt werden:
Der Minderleistungsfaktor ![]() liegt i.A. im Bereich von 0,5…0,75, nach anderen Angaben zwischen 0,65…0,85.
liegt i.A. im Bereich von 0,5…0,75, nach anderen Angaben zwischen 0,65…0,85.
(Bemerkung: Eine Streuung des Minderleistungsfaktors zwischen 0,5 und 0,85 ist viel zu groß, um einen exakten Außendurchmesser zu berechnen. Der Minderleistungsfaktor muss bei der hier vorgestellten Außendurchmesser-Berechnungsvorschrift wesentlich genauer bestimmt werden, siehe auch nachfolgenden Abschnitt 4.11.4.)
6. Ermittlung von ![]() nach Weber, F.J.: Arbeitsmaschinen: Kreiselpumpen und Verdichter, 2., verbesserte Ausgabe. VEB Verlag Technik Berlin 1962
nach Weber, F.J.: Arbeitsmaschinen: Kreiselpumpen und Verdichter, 2., verbesserte Ausgabe. VEB Verlag Technik Berlin 1962
Die Größe des Schaufelradaußendurchmessers ![]() und die Form der Schaufel am Austritt sind von der Förderhöhe H bzw. der spezifischen Stutzenarbeit Y abhängig. Das Schaufelradaustrittsdreieck muss der theoretischen Hauptgleichung für Strömungsmaschinen (Eulersche Hauptgleichung) entsprechen. Da mit
und die Form der Schaufel am Austritt sind von der Förderhöhe H bzw. der spezifischen Stutzenarbeit Y abhängig. Das Schaufelradaustrittsdreieck muss der theoretischen Hauptgleichung für Strömungsmaschinen (Eulersche Hauptgleichung) entsprechen. Da mit
![]()
nur das Produkt ![]() bekannt ist, für das Austrittsdreieck jedoch 3 Bestimmungsgrößen benötigt werden, müssen noch zwei weitere voneinander unabhängige Größen zur Durchmesserberechnung angenommen werden.
bekannt ist, für das Austrittsdreieck jedoch 3 Bestimmungsgrößen benötigt werden, müssen noch zwei weitere voneinander unabhängige Größen zur Durchmesserberechnung angenommen werden.
Diese angenommenen Kenngrößen sind die Meridiankomponente ![]() und der Austrittswinkel
und der Austrittswinkel ![]() .
.
Bei radialer Einströmung mit ![]() = 90° ist
= 90° ist ![]() .
.
Übliche Werte von ![]() gibt WEBER für Flüssigkeits- und Gasförderung mit
gibt WEBER für Flüssigkeits- und Gasförderung mit
![]()
an.
Der Austrittswinkel ![]() liegt im Regelfall zwischen 20°….50°, bekannt sind aber auch vor allem bei notwendigen Kennlinienanpassungen bei vorgegebenem Bauraum wesentlich größere Werte.
liegt im Regelfall zwischen 20°….50°, bekannt sind aber auch vor allem bei notwendigen Kennlinienanpassungen bei vorgegebenem Bauraum wesentlich größere Werte.
Aus der theoretischen Hauptgleichung in Förderhöhen-Schreibweise lässt sich unter Zuhilfenahme des Austrittsdreieckes die Umfanggeschwindigkeit ![]() berechnen:
berechnen:
Für ![]() =90° gilt
=90° gilt
![]()
und daraus
![]()
Man erhält für ![]() eine quadratische Gleichung, die auf die Normalform
eine quadratische Gleichung, die auf die Normalform
![]()
gebracht werden kann. Diese Gleichung nach ![]() [m/s] aufgelöst ergibt:
[m/s] aufgelöst ergibt:
für ![]() =90°
=90°
![Rendered by QuickLaTeX.com \[\boldsymbol {u_2^2=\frac{c_{m2}}{2\cdot tan\beta_2}+\sqrt{\left(\frac{c_{m2}}{2\cdot tan\beta_2}\right)^2+g\cdot H_{th\, \infty}}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-4fa778cf6aa983fe2ffb6a3b60952d9c_l3.png)
für ![]() ≠90°
≠90°
![Rendered by QuickLaTeX.com \[\boldsymbol {u_2^2=\frac{c_{m2}}{2\cdot tan\beta_2}+\sqrt{\left(\frac{c_{m2}}{2\cdot tan\beta_2}\right)^2+g\cdot H_{th\, \infty}+u_{1}\cdot c_0 \cdot cos\alpha_0}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-fb2ba45dbfc70b939d4a01ed7fbcf8f0_l3.png)
Die zweite Lösung dieser Gleichungen mit negativem Vorzeichen vor der Wurzel kann unberücksichtigt bleiben, da ![]() nicht negativ werden kann.
nicht negativ werden kann.
Nachteilig bei Verwendung obenstehender Gleichungen ist, dass darin nicht die gegebene Förderhöhe H, sondern die theoretische Förderhöhe für unendliche Schaufelzahl ![]() benötigt wird. Mit
benötigt wird. Mit
![]()
müssen zunächst der hydraulische Wirkungsgrad ![]() und der Minderleistungsfaktor
und der Minderleistungsfaktor ![]() abgeschätzt werden. Der hydraulische Wirkungsgrad
abgeschätzt werden. Der hydraulische Wirkungsgrad ![]() sollte je nach Pumpengröße im Bereich von 0,7…0,95 liegen. Der Minderleistungsfaktor kann aus empirisch gefundenen Beziehungen, wie im nachfolgenden Kapitel 4.11.4 dargestellt, ermittelt werden.
sollte je nach Pumpengröße im Bereich von 0,7…0,95 liegen. Der Minderleistungsfaktor kann aus empirisch gefundenen Beziehungen, wie im nachfolgenden Kapitel 4.11.4 dargestellt, ermittelt werden.
Aus der berechneten Umfangsgeschwindigkeit kann der Schaufelrad-Außendurchmesser berechnet werden:
![]()
7. Richtwerte nach DIN 24255
Für Schaufelraddurchmesser ab 125mm können die Richtwerte für die Außendurchmesser aus der DIN 24255 entnommen werden.