Für die Formgebung der Schaufeln sind der Eintrittswinkel ![]() und der Austrittswinkel
und der Austrittswinkel ![]() maßgebend. Es soll eine allmähliche Verringerung der Relativgeschwindigkeit von
maßgebend. Es soll eine allmähliche Verringerung der Relativgeschwindigkeit von ![]() auf
auf ![]() ohne Gefahr einer Strömungsablösung gewährleistet sein. Die Festlegung der Schaufelform erfolgt nach der zweidimensionalen Stromfadentheorie, bei der Gleichheit des Strömungszustandes über einen Parallelkreis angenommen wird. Diese Annahme trifft jedoch nur bei unendlicher Schaufelzahl zu und führt bei spezifischen Drehzahlen bis
ohne Gefahr einer Strömungsablösung gewährleistet sein. Die Festlegung der Schaufelform erfolgt nach der zweidimensionalen Stromfadentheorie, bei der Gleichheit des Strömungszustandes über einen Parallelkreis angenommen wird. Diese Annahme trifft jedoch nur bei unendlicher Schaufelzahl zu und führt bei spezifischen Drehzahlen bis ![]() ≈ 50 zu guten Ergebnissen.
≈ 50 zu guten Ergebnissen.
a) Festlegung der Schaufelform aus einem Kreisbogen nach Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg
Die Schaufelform als Kreisbogen stellt die einfachste Konstruktionsvariante dar. Die Schaufeln können rückwärts- sowie vorwärtsgekrümmt ausgeführt werden. Die Kreisbogenschaufel erhält eine konstante Krümmung R:
![]()
Der geometrische Ort der Krümmungsmittelpunkte ist der Radius ![]() und wird bestimmt mit:
und wird bestimmt mit:
![]()
Der Zentriwinkel ![]() errechnet sich aus:
errechnet sich aus:
![]()
b) Festlegung der Schaufelform aus zwei Kreisbögen
Die Schaufelkonstruktion aus zwei Kreisbögen kann aus Weber, F.J.: Arbeitsmaschinen: Kreiselpumpen und Verdichter, 2., verbesserte Ausgabe. VEB Verlag Technik Berlin 1962 und aus Bommes, L.; Kramer, C. u.a.: Ventilatoren. expert-verlag 1990. S224/226. entnommen werden.
c) Punktweise Berechnung der Schaufel nach Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg
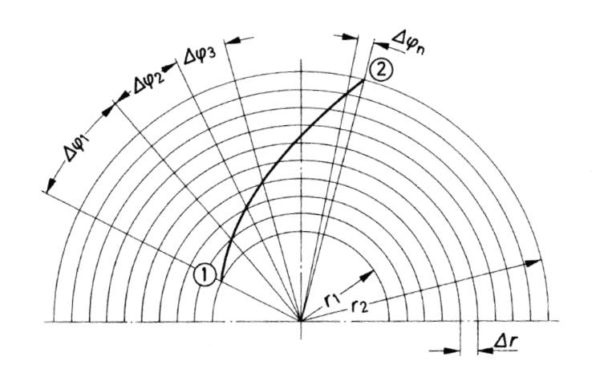
Die punktweise konstruierte Schaufel besteht nicht aus Kreisbögen, sondern wird in ihrer ganzen Länge festgelegt. Die einzelnen Punkte der Schaufeln werden im Polarkoordinatensystem dargestellt, d.h. es werden jeweils zu einem beliebigen Radius r der entsprechende Winkel ![]() (vom Anfangspunkt A der Schaufel aus gemessen) berechnet.
(vom Anfangspunkt A der Schaufel aus gemessen) berechnet.
![]()
Der Abstand zwischen ![]() und
und ![]() wird in eine Anzahl gleicher Intervalle
wird in eine Anzahl gleicher Intervalle ![]() unterteilt:
unterteilt:
![]()
Für die Darstellung einer beliebigen Schaufelkontur in Polarkoordinaten r und ![]() ergibt sich folgendes Verfahren:
ergibt sich folgendes Verfahren:
Unter der Annahme, dass die Funktion ![]() = f(r) linear verläuft, kann die Integration von
= f(r) linear verläuft, kann die Integration von
![]()
nummerisch erfolgen. Nun kann für jeden Radius r ein Winkel ![]() bestimmt werden.
bestimmt werden.
Für i=1 bis Anzahl werden folgende 3 Rechenschritte durchgeführt:
![]()
![]()
![]()
In der Ausgabe 2013 Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg wird ein von diesen Vorschriften abweichender Rechenweg unter Nutzung der Funktion
![]()
angegeben und kann ggf. dort herausgesucht werden.
Der Gesamtwinkel ergibt sich dann zu:
![Rendered by QuickLaTeX.com \[\boldsymbol {\varphi=\sum_{i=1}^{Anzahl} \Delta \varphi_i}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-0600e321063d08410e9ab676b53e1aaa_l3.png)
 d) Punktweise Berechnung der Schaufel nach Weber, F.J.: Arbeitsmaschinen: Kreiselpumpen und Verdichter, 2., verbesserte Ausgabe. VEB Verlag Technik Berlin 1962
d) Punktweise Berechnung der Schaufel nach Weber, F.J.: Arbeitsmaschinen: Kreiselpumpen und Verdichter, 2., verbesserte Ausgabe. VEB Verlag Technik Berlin 1962
Bei Flüssigkeitsförderung, also bei üblicher starker Rückwärtskrümmung der Schaufeln, hat sich der lineare ![]() – und w-Verlauf bewährt. Die Meridiangeschwindigkeiten
– und w-Verlauf bewährt. Die Meridiangeschwindigkeiten ![]() und
und ![]() und die Winkel
und die Winkel ![]() und
und ![]() sind aus der Entwurfsrechnung bekannt, die Relativgeschwindigkeiten
sind aus der Entwurfsrechnung bekannt, die Relativgeschwindigkeiten ![]() und
und ![]() lassen sich über das rechtwinklige Dreieck berechnen:
lassen sich über das rechtwinklige Dreieck berechnen:
![]()
![]()
![]()
![]()
Für i=1 bis Intervallanzahl werden folgende Rechenschritte durchgeführt:
Aus ![]() und w kann jeweils über
und w kann jeweils über ![]() =
= ![]() der Wert
der Wert ![]() ermittelt werden:
ermittelt werden:
![Rendered by QuickLaTeX.com \[\boldsymbol {\tan\beta_i=\frac{\left(c_{mi}/w_i\right)}{\sqrt{1-\left(c_{mi}/w_i\right)^2}}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-14f6357caabbaca5b008ab32358a1a6b_l3.png)
Für die Berechnung des Integrals bestimmt man zunächst die Werte ![]() :
:
![]()
Das Integral selbst wird als Summe schmaler Flächenstreifen aufgefasst, die als Abszisse den Zuwachs dr und als Ordinate die Werte der jeweiligen Funktion B haben. Ein Flächenstreifen hat demnach folgenden Flächeninhalt:
![]()
Zur Bestimmung des Winkels ![]() muss nur noch die Summe aller
muss nur noch die Summe aller ![]() von
von ![]() bis
bis ![]() gebildet werden und mit 180/
gebildet werden und mit 180/ ![]() multipliziert werden:
multipliziert werden:
![Rendered by QuickLaTeX.com \[\boldsymbol {\varphi_i=\frac{180}{\pi}\cdot\sum_{r_1}^{r_i}\Delta f_i}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-6372c1a0b25e921cb0f71e78e3bd2321_l3.png)
Die berechnete Schaufelform stellt die Arbeitskante der Schaufel dar. Die Schaufeldicke wird auf der Rückseite aufgetragen.
Man kann die errechnete Linie als Mittellinie (neutrale Faser) der Schaufel auffassen.