4.2 Hauptabmessungen und Kennzahlen von Kreiselpumpen

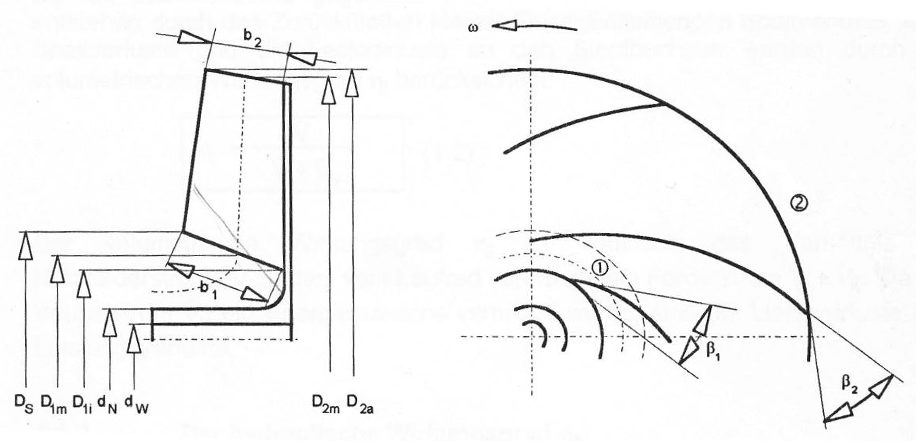
Hauptabmessungen  am Schaufelrad von radialen Kreiselpumpen

Die in den nachfolgenden Kapiteln genutzten Hauptabmessungen und Bezeichnungen am Schaufelrad sollen hier dargestellt werden:

D_S   Saugmunddurchmesser D_{1m}   mittlerer Innendurchmesser
D_{1i}   innerer Eintrittsdurchmesser Schaufel d_{n}   Nabendurchmesser
d_{W}   Wellendurchmesser b_{1}   Schaufelbreite am Radeinlass
b_{2}   Schaufelbreite am Radauslass D_{2m}   mittlerer Außendurchmesser
D_{2a}   Schaufelradaußendurchmesser \beta_{1}   Schaufeleintrittswinkel
\beta_{2}   Schaufelaustrittswinkel \omega   Winkelgeschwindigkeit, Drehrichtung
1   Eintritt ins Schaufelrad 2   Austritt aus dem Schaufelrad

Die allgemein üblichen Bezeichnungen 1 für Eintritt und 2 für Austritt reichen oft nicht aus, um die Verhältnisse an Eintritt und Austritt strömungstechnisch exakt zu beschreiben. Deshalb werden folgende präzisere Stellenindizes eingeführt:

0   Stelle unmittelbar vor dem Eintritt in den Schaufelkanal
1   Stelle unmittelbar hinter dem Eintritt in den Schaufelkanal
2   Stelle unmittelbar vor dem Austritt aus den Schaufelkanal
3   Stelle unmittelbar hinter dem Austritt aus den Schaufelkanal

Die Stellen 0 und 1 liegen dabei auf dem gleichen Eintritts- und die Stellen 2 und 3 auf dem gleichen Austrittsdurchmesser. Die Unterscheidung der einzelnen Stellen ergibt sich aus der wegen der endlichen Dicke der Schaufeln resultierenden Querschnittsverengung.

Gelegentlich werden die Stellen im Schaufelkanal mit i und außerhalb mit a gekennzeichnet, also 1i für Stelle 1 innen, 1a für Stelle 1 außen und analog die Stelle 2.

Die Radschaufeln werden in der sog. Zirkularprojektion (Meridianschnitt) dargestellt. Dabei wird jeder dreidimensionale Punkt der Schaufel auf seinem entspechenden Radius in die höchste Stelle gedreht und dann in die Schnittdarstellung projiziert. Am Eintrittsdurchmesser D_1 beginnen die Radschaufeln und enden am Austrittsdurchmesser D_2.

 

Kennzahlen von Kreiselpumpen

Im Strömungsmaschinenbau werden oft die dimensionslosen Kennzahlen zur Darstellung von Versuchswerten und bei der Auslegungsberechnung verwendet. Diese Kennzahlen werden  nachfolgend aufgeführt und erläutert. Zu diesem und vielen anderen, auch auf dieser Website diskutierten, das Schaufelrad von Arbeitsmaschinen betreffende Themen sei das Fachbuch  Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg empfohlen. Teile der Kapitel 4 und 5 werden mit freundlicher Genehmigung  des Vogel Buchverlages Würzburg diesem Fachbuch entnommen und speziell für Kraftfahrzeugpumpen diskutiert.

Da die dimensionslosen Kenngrößen nicht nur wie in folgender Auflistung mithilfe der spezifischen Förderenergie Y, sondern oft auch mit den Kenngrößen Förderhöhe H und Gesamtdruckdifferenz nach Bernoulli \Delta p_{ges} dargestellt werden, an dieser Stelle  die Beziehungen zwischen diesen Größen, siehe auch nachfolgendes Kapitel 4.3:

    \[\boldsymbol {Y=H \cdot g=\frac{\Delta p_{ges}}{\varrho}}\]

wobei Y als spezifische Förderenergie oder üblicherweise als spezifische Stutzenarbeit der Strömungsmaschine bezeichnet wird.

Kennzahlen von Arbeitsmaschinen, nach Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg
Kennzahlen von Arbeitsmaschinen, nach Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg

 

!Die spezifische Drehzahl n_q wird meist noch zur Charakterisierung von Strömungsmaschinen genutzt. International gibt es aber unterschiedliche Definitionen zur Berechung der spezifischen Drehzahl. Deshalb sollte dazu übergegangen werden, statt der spezifischen Drehzahl die Laufzahl zu verwenden!formelzeichen 4 2

Druckzahl ψ:
Die schon seit langem bei Strömungsmaschinen benutzte Druckzahl ψ bezieht die spezifische Förderenergie (spezifische Stutzenarbeit) Y auf das Quadrat der Umfangsgeschwindigkeit u:

    \[\boldsymbol {\psi=\frac{2 \cdot Y}{u^{2}}=\frac{2 \cdot Y}{D^{2}\cdot \pi^{2}\cdot n^{2}}}\]

Für die Festlegung der Bezugsumfangsgeschwindigkeit konnte noch keine Vereinheitlichung erzielt werden. Üblicherweise ist u die Umfangsgeschwindigkeit des Arbeitsmediums am Schaufelradaustritt. Bei der Benutzung von Versuchswerten und Kennfeldern ist deshalb immer auf die betreffende Festlegung der Umfangsgeschwindigkeit zu achten.

Durchflusszahl φ:
Die Durchflusszahl φ, manchmal auch Lieferzahl oder Volumenzahl genannt, ist ursprünglich als Verhältnis von Meridiangeschwindigkeit c_m zur Umfangsgeschwindigkeit u definiert:

    \[\boldsymbol {\varphi=\frac{c_{m}}{u}}\]

Da die Meridiangeschwindigkeit c_m proportional zum Volumenstrom \dot V und dem Strömungsquerschnitt A ist, gilt folgendes:

    \[\boldsymbol {\text {allgemein: }\,\,\, \,\,\, c_{m}=\frac{4\cdot \dot{V}}{\pi \cdot D^{2}}}\]

    \[\boldsymbol {\text {speziell f\"ur ein Pumpenrad mit $A=\pi \cdot b \cdot D$:} \,\,\, \,\,\, c_{m}=\frac{\dot{V}}{\pi\cdot b_{2}\cdot D_{2}}}\]

mit D_2 als Schaufelraddurchmesser und b_2 als Schaufelbreite am Auslass. Für die Umfangsgeschwindigkeit u gilt:

    \[\boldsymbol {u=r_{2}\cdot \omega=D_{2}\cdot \pi \cdot n}\]

Damit wird die Durchflusszahl φ zu:

    \[\boldsymbol {\text {allgemein: }\,\,\, \,\,\, \varphi=\frac{4 \cdot \dot{V}}{D^{3}\cdot \pi^{2}\cdot n}}\]

    \[\boldsymbol {\text {f\"ur ein radiales Pumpenrad:} \,\,\, \,\,\,\,\,\, \varphi=\frac{\dot{V}}{D_2^2\cdot \pi^2 \cdot b_{2}\cdot n}}\]

Leistungszahl λ:
Die Leistung einer Strömungsmaschine ist proportional zum Volumenstrom \dot V, zur spezifischen Förderenergie Y und zum Gesamtwirkungsgrad \eta_{ges}. Da der Volumenstrom \dot V proportional zur Durchflusszahl φ und die spezifische Förderenergie Y proportional zur Druckzahl ψ sind, kann auch die Leistung P durch eine Leistungszahl λ dimensionslos ausgedrückt werden. Für eine Pumpe (Arbeitsmaschine) gilt:

    \[\boldsymbol {\lambda=\frac{\varphi\cdot\psi}{\eta_{ges}}}\]

Setzt man in diese Formel die entsprechenden Beziehungen für die Druckzahl ψ und die Durchflusszahl φ, dann ergibt sich:

    \[\boldsymbol {\text {allgemein: }\qquad \lambda=\frac{4\cdot \dot{V}\cdot 2\cdot Y}{\eta_{ges} \cdot D^{3}\cdot \pi^2 \cdot n \cdot u_{2}} }}\]

    \[\boldsymbol {\text {f\"ur ein radiales Pumpenrad:} \qquad\lambda=\frac{\dot{V}\cdot 2 \cdot Y}{\eta_{ges}\cdot D_2^2 \cdot \pi^2 \cdot b_{2}\cdot n \cdot u^{2}} }}\]

    \[\boldsymbol {\text {Da f\"ur} \qquad {P_{An}=\frac{\dot{V}\cdot Y\cdot \varrho}{\eta_{ges}} \qquad\text {und f\"ur} \qquad u^{2}=D^{2}\cdot \pi^2\cdot n_{2}}}\]

gesetzt werden kann, ergibt sich folgende Definition für die Leistungszahl λ, ausgedrückt durch die Antriebsleistung P_{An}:

    \[\boldsymbol {\text {allgemein: }\qquad \lambda=\frac{8\cdot P_{An}}{D^{5}\cdot \pi^4 \cdot n^{3}\cdot \varrho} }}\]

    \[\boldsymbol {\text {f\"ur ein radiales Pumpenrad:} \qquad \lambda=\frac{2\cdot P_{An}}{D_2^4 \cdot \pi^4 \cdot b_{2}\cdot n_{3}\cdot \varrho} }}\]

Laufzahl σ:
Durch Auflösen der Berechnungsgleichungen zur Ermittlung der Druckzahl ψ und der Durchflusszahl φ (siehe oben) nach den Durchmesser D erhält man:

    \[\boldsymbol {\psi=\frac{2\cdot Y}{u^{2}}=\frac{2\cdot Y}{D^{2}\cdot \pi^{2}\cdot n^{2}}\qquad\Rightarrow\qquad D=\frac{\left(2\cdot Y\right)^{1/2}}{n\cdot \pi \cdot \psi^{1/2}}}\]

    \[\boldsymbol {\varphi=\frac{4\cdot \dot V}{D^{3}\cdot \pi^{2} \cdot n}\qquad\Rightarrow\qquad D=\frac{\left(4\cdot \dot V\right)^{1/3}}{\pi^{2/3}\cdot \varphi^{1/3}\cdot n^{1/3}}}\]

Durch Gleichsetzen beider Formeln wird D eliminiert:

    \[\boldsymbol {\frac{\left(2\cdot Y\right)^{1/2}}{n\cdot \pi \cdot \psi^{1/2}}=\frac{\left(4\cdot \dot V\right)^{1/3}}{\pi^{2/3}\cdot \varphi^{1/3}\cdot n^{1/3}}}\]

    \[\boldsymbol {n^{2/3}=\frac{\left(2 \cdot Y\right)^{1/2}\cdot \varphi^{1/3}}{\left(4\cdot \dot V\right)^{1/3}\cdot \psi^{1/2}\cdot \pi^{1/3}}}\]

    \[\boldsymbol {n=\frac{\left(2\cdot Y\right)^{3/4}\cdot \varphi^{1/2}}{\left(4\cdot \dot V\right)^{1/2}\cdot \psi^{3/4}\cdot \pi^{1/2}}}\]

Für den Ausdruck \varphi^{1/2} /\psi^{3/4} wird eine dimensionslose Kennzahl, die Laufzahl σ eingeführt:

    \[\boldsymbol {\sigma=\frac{\varphi^{1/2}}{\psi^{3/4}}}\]

Die Laufzahl σ durch n, \dot V und Y ausgedrückt, ergibt sich:

    \[\boldsymbol {\sigma=n\cdot \frac{\sqrt{\dot V}}{\left(2 \cdot Y\right)^{3/4}}\cdot 2 \cdot \sqrt{\pi}}\]

Mit Einschränkungen lassen sich den Laufzahlen bestimmte Schaufelradformen zuordnen. Radial-Schaufelrädern ist eine Laufzahl von 0,06…0,32 zugeordnet. Werte über 0,32 gehören bereits zum Diagonalrad. Zur Erzielung von hohen Wirkungsgraden sollten keine zu kleinen Laufzahlen gewählt werden.

Spezifische Drehzahl n_q :
Wie oben bereits erwähnt, wird oftmals noch statt der Laufzahl die Kenngröße spezifische Drehzahl n_q verwendet. Sie errechnet sich aus:

    \[\boldsymbol {n_{q}=n\cdot \frac{\sqrt{\dot V}}{H^{0,75}}=5.542\cdot n \cdot \frac{\sqrt{\dot V}}{Y^{0,75}}}\]

Es ist darauf zu achten, dass bei Berechnungen  und Schaufelradauslegungen die Kenngrößen Laufzahl und spezifische Drehzahl nicht verwechselt werden. In Beziehung stehen Laufzahl und spezifische Drehzahl mit:

    \[\boldsymbol {\sigma=\frac{n_q}{157.8}}\]

Durchmesserzahl δ:
Durch Eliminieren der Drehzahl n aus den Berechnungsformeln zur Ermittlung der Kenngrößen Druckzahl ψ und Durchflusszahl φ sowie entsprechendes Umformen erhält man:

    \[\boldsymbol {\frac{\left(2\cdot Y\right)^{1/2}}{D\cdot \pi\cdot \sqrt{\psi}}=\frac{4\cdot \dot V}{D^{3}\cdot \pi^{2}\cdot \varphi}}\]

    \[\boldsymbol {D=\frac{2}{\sqrt{\pi}}\cdot\sqrt{\dot V}\cdot \left(2\cdot Y\right)^{1/4}\cdot \frac{\psi^{1/4}}{\varphi^{1/2}}}\]

Für den Quotienten \frac{\psi^{1/4}}{\varphi^{1/2}} wird die dimensionslose Durchmesserzahl δ gesetzt:

    \[\boldsymbol {\delta=\frac{\psi^{1/4}}{\varphi^{1/2}}}\]

 Mit den Hauptbetriebsdaten \dot V, Y und D ausgedrückt, ergibt sich:

    \[\boldsymbol {\delta=D\cdot \sqrt[4]{\frac{2 \cdot Y}{\dot V^{2}} }\cdot \frac{\sqrt{\pi}}{2}}\]

 

nächstes Kapitel