Verlauf der theoretischen Kennlinie
- Bei radial endenden Schaufeln (
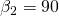 ) verläuft die theoretische Kennlinie als parallele Gerade zur x-Achse.
) verläuft die theoretische Kennlinie als parallele Gerade zur x-Achse. - Bei vorwärts gekrümmten Schaufeln (
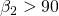 ) steigt mit zunehmendem Förderstrom die theoretische Förderhöhe linear an.
) steigt mit zunehmendem Förderstrom die theoretische Förderhöhe linear an. - Bei rückwärts gekrümmten Schaufeln (
 ) fällt die theoretische Förderhöhe mit steigendem Förderstrom linear ab.
) fällt die theoretische Förderhöhe mit steigendem Förderstrom linear ab.
Für die theoretische spezifische Stutzenarbeit ![]() und die theoretische Förderhöhe
und die theoretische Förderhöhe ![]() ergeben sich somit folgende Kennlinienverläufe:
ergeben sich somit folgende Kennlinienverläufe:
Radial endende Schaufelräder werden praktisch bei Kfz-Kühlmittelpumpen nicht mehr verwendet. Die übliche Bauweise ist mit rückwärts gekrümmten Schaufeln, mitunter werden vorwärts gekrümmte Schaufeln konstruiert, um bei begrenztem bzw. vorgegebenem Bauraum die Pumpenkennlinie z.B. für leistungsgesteigerte Motorenversionen anzuheben:
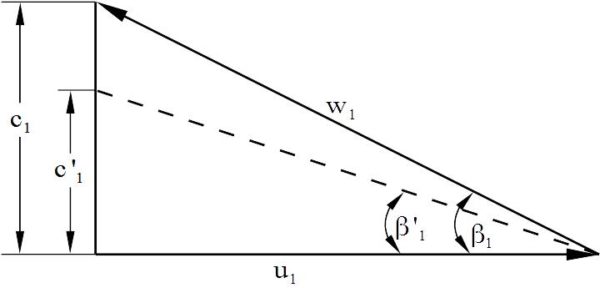
Die Verläufe der theoretischen Kennlinie leiten sich aus der theoretischen Hauptgleichung ab. Diese Eulersche Strömungsmaschinen-Hauptgleichung
![]()
wird unter der Annahme von ![]() =90° und damit
=90° und damit ![]() =0 im Rechnungspunkt, durch Winkelbeziehungen und Geschwindigkeiten im Geschwindigkeitsdreieck am Schaufelradeintritt und am Schaufelradaustritt sowie mit
=0 im Rechnungspunkt, durch Winkelbeziehungen und Geschwindigkeiten im Geschwindigkeitsdreieck am Schaufelradeintritt und am Schaufelradaustritt sowie mit
![]()
und der Kontinuitätsgleichung
![]()
zu folgender Gleichung:
![]()
Theoretische Hauptgleichung für Strömnungsmaschinen und Geschwindigkeitsdreiecke werden in den nachfolgenden Kapiteln ausführlicher betrachtet.
Unter Annahme unendlich dünner Schaufeln kann zur Berechnung der theoretisch möglichen Förderarbeit der Faktor ![]() zunächst mit 1 angesetzt werden.
zunächst mit 1 angesetzt werden.
Mit ![]() als Variable ergibt sich im
als Variable ergibt sich im ![]() -Diagramm eine Gerade, deren Anstieg von
-Diagramm eine Gerade, deren Anstieg von ![]() abhängt. Setzt man
abhängt. Setzt man ![]() =0, dann erhält man den theoretischen Anspringpunkt der Pumpe. Bei Verwendung der Förderhöhe H errechnet sich dieser Punkt aus
=0, dann erhält man den theoretischen Anspringpunkt der Pumpe. Bei Verwendung der Förderhöhe H errechnet sich dieser Punkt aus ![]() . Bei Verwendung der spezifischen Förderenergie ist dieser Punkt
. Bei Verwendung der spezifischen Förderenergie ist dieser Punkt ![]() , da der rechte Term in der obigen Gleichung für
, da der rechte Term in der obigen Gleichung für ![]() bei
bei ![]() =0 ebenfallls 0 wird.
=0 ebenfallls 0 wird. Verlauf der wirklichen Kennlinie
Verlauf der wirklichen Kennlinie
Die wirklichen, auf dem Pumpenprüfstand ermittelten Kennlinien der Kühlmittelpumpe (Drosselkurven) weichen sehr stark von den theoretischen Kennlinien ab. Dies resultiert daraus, dass zur Berechnung der theoretischen Kennlinie reibungs- und stoßverlustfreie Strömungen sowie eine unendliche Schaufelzahl vorausgesetzt wurden. Außerdem wird angenommen, dass die Schaufelwinkel dem jeweiligen relativen Strömungszustand bzw. der Relativströmung entsprechen.
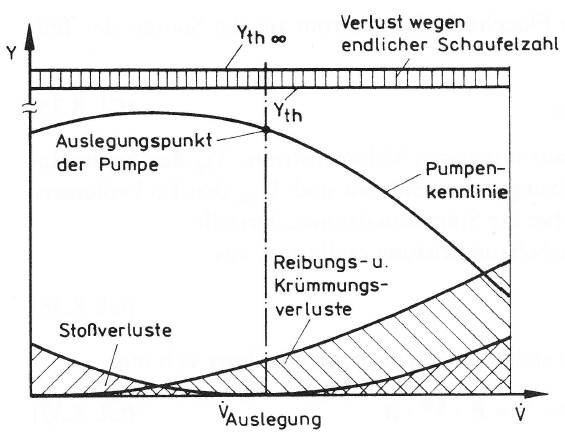
Die wirkliche Kennlinie erhält man folgendermaßen (das Beispiel ist für radial endende Schaufeln dargestellt, gilt aber ebenso für vorwärts und rückwärts gekrümmte Schaufeln):
Schaufeln
–
–
-
-
- 1. Durch den Einfluss der endlichen Schaufelzahl ergibt sich eine Minderleistung des Schaufelrades, die Kennlinie wird dadurch von
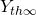 auf
auf 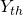 gesenkt.
gesenkt.
- 1. Durch den Einfluss der endlichen Schaufelzahl ergibt sich eine Minderleistung des Schaufelrades, die Kennlinie wird dadurch von
-
- 2. Die Reibungs- und Krümmungsverluste nehmen mit zunehmender Strömungsgeschwindigkeit quadratisch zu. Diese Verluste werden bei der Ermittlung der wirklichen Kennlinie von
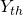 bei gleichen Volumenströmen abgezogen.
bei gleichen Volumenströmen abgezogen. - 3. Die Stoßverluste am Eintritt sowie die Umlenkverluste am Austritt zur Leiteinrichtung, z.B. zum Spiralkanal, verlaufen angenähert einer Parabel (Kurve ‘Stoßverluste’), deren Scheitelpunkt auf der X-Achse beim Auslegungsvolumenstrom liegt. Diese Stoß- und Umlenkverluste zieht man bei gleichen Volumenströmen von der aus 2. resultierenden Kurve ab und man erhält die wirkliche Kennlinie (‘Pumpenkennlinie’).
- 2. Die Reibungs- und Krümmungsverluste nehmen mit zunehmender Strömungsgeschwindigkeit quadratisch zu. Diese Verluste werden bei der Ermittlung der wirklichen Kennlinie von
-
Am Schaufelradeintritt hat die Strömung beim Nennförderstrom bzw. Auslegungsförderstrom die Richtung des Eintrittswinkels ![]() . Bei vom Auslegungsvolumenstrom abweichenden Fördermengen ändert sich der Strömungswinkel. Er stimmt dann mit der Schaufelrichtung nicht mehr überein und als Folge treten am Eintritt Stoßverluste auf (Bild: Schaufelstoß am Eintritt).
. Bei vom Auslegungsvolumenstrom abweichenden Fördermengen ändert sich der Strömungswinkel. Er stimmt dann mit der Schaufelrichtung nicht mehr überein und als Folge treten am Eintritt Stoßverluste auf (Bild: Schaufelstoß am Eintritt).
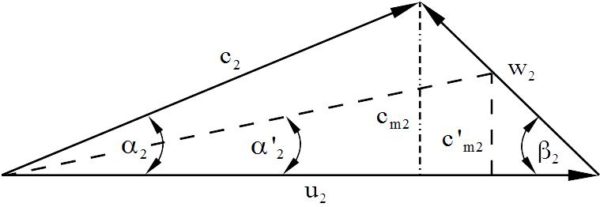
Am Schaufelradaustritt bleibt der Winkel ![]() der Strömung aufgezwungen. Die Meridiankomponente
der Strömung aufgezwungen. Die Meridiankomponente ![]() ändert sich jedoch bei verändertem Förderstrom. Dadurch ändert sich der Winkel
ändert sich jedoch bei verändertem Förderstrom. Dadurch ändert sich der Winkel ![]() und beim Übertritt der Strömung in die Leiteinrichtung (Spiralkanal) entstehen Umlenkverluste (Bild: Abgelenkte Strömung am Austritt).
und beim Übertritt der Strömung in die Leiteinrichtung (Spiralkanal) entstehen Umlenkverluste (Bild: Abgelenkte Strömung am Austritt).
Das Kennlinienfeld der Kühlmittelpumpe
Die Linien, welche in einem Diagramm die Förderhöhe, die spezifische Stutzenarbeit oder den Differenzdruck in Abhängigkeit vom Förderstrom darstellen, werden Kennlinien oder Drosselkurven genannt, weil sie durch Drosselung der Regelschieber am Pumpenprüfstand bei konstanter Drehzahl ermittelt werden.
Für unterschiedliche Drehzahlen erhält man verschiedene Kennlinien, welche über die sogenannten Proportionalitätsgesetzte für Kreiselpumpen untereinander berechenbar sind, d.h. das man aus einer Kennlinie die Kennlinien für andere Drehzahlen berechnen kann, siehe auch Kap. 4.6.
Bei Konstanthaltung der Drehzahl und Drosselung des Volumenstromes ergibt sich das charakteristische Kennfeld, das sog. Drosselkennfeld, der Kühlmittelpumpe.
Werden in das Kennfeld noch die Punkte gleichen Wirkungsgrades eingezeichnet, so ergeben die Verbindungslinien der gleichen Wirkungsgrade eiförmige Kurven, die sogenannten Muschelkennlinien. Voraussetzung zur Ermittlung dieser Muschelkennlinien ist die Messung der Antriebsleistung der Kühlmittelpumpe (genau genommen lässt sich die Antriebsleistung nicht direkt messen, sondern aus dem messtechnisch ermittelten Drehmoment und der zugehörigen Drehzahl errechnen). Stimmen der Auslegungspunkt der Pumpe mit dem messtechnisch ermittelten Arbeitspunkt der Pumpe, also dem Schnittpunkt aus Auslegungsdrehzahl und Kühlkreislaufwiderstand, genau überein, so sollte bei einer strömungstechnisch korrekt ausgelegten Pumpe in diesem Schnittpunkt auch das Wirkungsgradmaximum liegen. Nachfolgendes Bild zeigt schematisch solch ein Kennfeld bei Verwendung der Pumpenkenngröße spezifische Förderenergie Y:
Zu beachten ist, dass die Pumpendrehzahlen bei der Kennfeldermittlung so ausgewählt werden, dass die Drehzahlen für einzelne Motorbetriebszustände abgedeckt werden, z.B. Leerlaufdrehzahl, Drehzahl für maximales Drehmoment, Auslegungsdrehzahl (oft Drehzahl für maximale Motorleistung), Abregeldrehzahl; alle Drehzahlen unter Beachtung des Übersetzungsverhältnisses von Motor zur Kühlmittelpumpe. Geeignete Zwischenabstufungen der Pumpendrehzahlen sind entsprechend zu wählen.
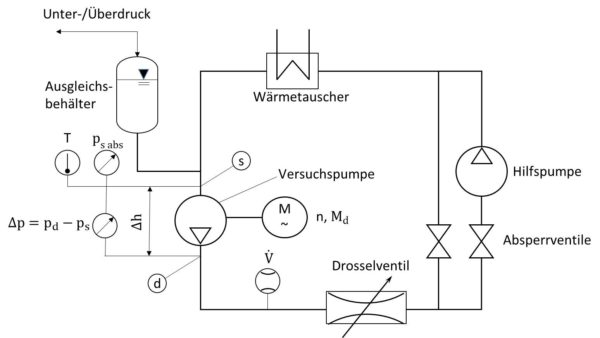
Die Pumpenkennfelder werden auf einem Prüfstandsaufbau wie im Bild unten schematisch dargestellt ermittelt:
Mit der Hilfspumpe im Prüfstandsaufbau oben wird der Anlagenwiderstand des Prüfstandes überwunden, der u.U. größer sein kann als der Kühlkreislaufwiderstand, so dass die auf dem Pumpenrüfstand ermittelten Pumpenkennlinien ohne Hilfspumpe schon vor dem Auslegungspunkt enden würden.
Für die Pumpenkenngrößen Pumpendifferenzdruck ![]() , Förderhöhe H und spezifische Förderenergie Y gelten dabei folgende Berechnungsvorschriften, siehe auch Kap. 1.1:
, Förderhöhe H und spezifische Förderenergie Y gelten dabei folgende Berechnungsvorschriften, siehe auch Kap. 1.1:
Pumpendifferenzdruck [N/m², Pa, mbar, bar]:
Die Berechnung des Pumpendifferenzdruckes ![]() ergibt sich aus der Druckgleichung nach Bernoulli. Man erhält den Gesamtdruck nach Bernoulli bzw. den Gesamtdifferenzdruck nach Bernoulli
ergibt sich aus der Druckgleichung nach Bernoulli. Man erhält den Gesamtdruck nach Bernoulli bzw. den Gesamtdifferenzdruck nach Bernoulli ![]() , da der Druck aus der Summe von statischem und dynamischem Druckanteil gebildet wird:
, da der Druck aus der Summe von statischem und dynamischem Druckanteil gebildet wird:
![]()
![Rendered by QuickLaTeX.com \[\boldsymbol {\Delta p_{Pumpe}=p_{ges\textbf{ }d}-p_{ges\textbf{ }s}=\left ( p_{d}-p_{s} \right )+\varrho \cdot g\cdot \left ( h_{d}-h_{s} \right )+\varrho \cdot \left ( \frac{c\tfrac{2}{d}}{2}- \frac{c\tfrac{2}{s}}{2}\right )}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-08b84930ff0e5850c627239455113792_l3.png)
Sind die Flüssigkeitssäulen auf die Druckmessgeräte (Druckgeber) gleich hoch, so entfällt der Höhenanteil der Druckgleichung. Sind die Strömungsdurchmesser der Druckmessstellen von Pumpendruckseite und Pumpensaugseite gleich, so heben sich die dynamischen Druckanteile von Saugseite und Druckseite auf. Anderenfalls sind die dynamischen Druckanteile zur Berechnung des Pumpendifferenzdruckes unbedingt zu beachten.
Der Kennlinienverlauf bei Verwendung der Pumpenkenngröße ![]() ist abhängig von der Fluidtemperatur und der Fluidzusammensetzung, d.h. verschiedene Temperaturen und unterschiedliche Frostschutzanteile ergeben abweichende Kennlinien.
ist abhängig von der Fluidtemperatur und der Fluidzusammensetzung, d.h. verschiedene Temperaturen und unterschiedliche Frostschutzanteile ergeben abweichende Kennlinien.
Pumpenförderhöhe [m]:
Um eine fluidtemperaturunabhängige und fluidzusammensetzungsunabhängige Darstellung des Kennfeldes zu erhalten, wird die Kenngröße Förderhöhe H eingeführt:
![]()
Die Pumpenförderhöhe H gilt also, ebenso wie die spezifische Förderenergie Y, für alle Temperaturen und Zusammensetzungen.
Spezifische Förderenergie bzw. spezifische Stutzenarbeit [Nm/kg][J/kg]:
Die Pumpenkenngröße spezifische Förderenergie ist eine SI-Einheit und unterscheidet sich von der Förderhöhe lediglich durch die Erdbeschleunigung g:
![]()
Zu beachten ist, dass die oftmals auftretende Angabe des Pumpenauslegungspunktes als Druck und Volumenstrom nicht korrekt ist, da die ermittelten Kennlinien dann von Temperatur und Zusammensetzung abhängig sind. Es müsste zumindest eine dazugehörige Fluiddichte mit angegeben werden, bei welcher dieser Pumpendifferenzdruck gilt. Strömungstechnisch korrekt ist die Angabe des Auslegungspunktes in Förderhöhe H oder spezifischer Stutzenarbeit Y jeweils mit dem Volumenstrom.
Stabiler und labiler Kennlinienverlauf
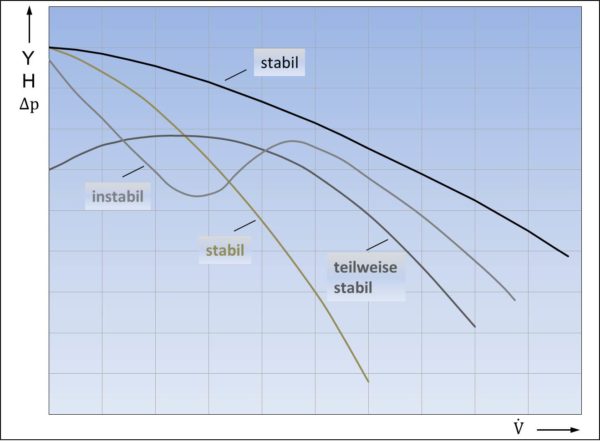
Die Kennlinien im Pumpenkennfeld können einen stabilen oder einen labilen Verlauf aufweisen. Pumpen mit labilem Kennlinienverlauf können im Betrieb undefinierte Zustände einnehmen, deshalb sollten die Pumpenkennlinien immer einen stabilen Verlauf aufweisen. In Gebr. Sulzer AG: Kreiselpumpenhandbuch, Vulkan Verlag 1990 und Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg sind einige Beispiele für stabile und labile Kurvenverläufe dargestellt. Dabei ist allerdings zu beachten, dass sich für Kfz-Kühlmittelpumpen etwas andere Verhältnisse als bei großen Anlagenpumpen ergeben, da sich im PKW-Kühlkreislauf regelungsbedingt maximale und minimale Kreislaufströmungswiderstände ergeben. Im Bild unten schematisch stabile und labile Kurvenverläufe:
Die beiden stabilen Kennlinienarten sind im KfZ-Kühlmittelpumpenbau übliche Kurvenverläufe. Auch der als teilweise stabile Kennlinienverlauf ist oft bei Kfz-Kühlmittelpumpen zu sehen, d.h. es erfolgt ab dem Anspringpunkt der Pumpe (![]() ) ein leichter Kennlinienanstieg, um dann ab dem Scheitelpunkt kontinuierlich abzufallen. Da der Kreislaufregelbereich weit außerhalb des Kennlinienanstieges liegt, wird dieser Verlauf als unkritisch angesehen.
) ein leichter Kennlinienanstieg, um dann ab dem Scheitelpunkt kontinuierlich abzufallen. Da der Kreislaufregelbereich weit außerhalb des Kennlinienanstieges liegt, wird dieser Verlauf als unkritisch angesehen.
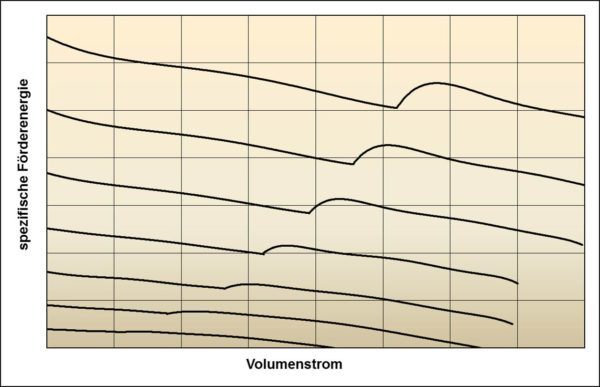
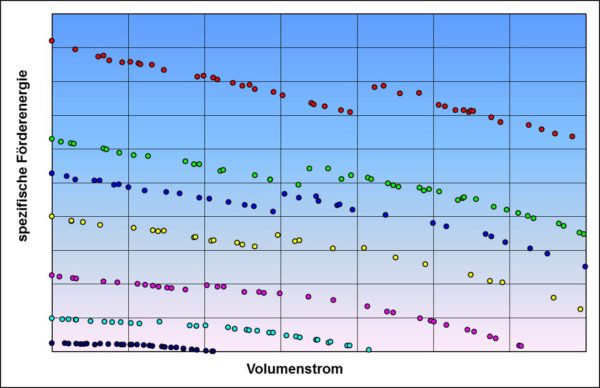
Anders verhält es sich mit dem instabilen Kurvenverlauf. Solche Pumpenkennlinien sind unbedingt zu vermeiden, da im Bereich zwischen maximalen und minimalen Kühlkreislaufwiderständen, z.B. bei Thermostatregelung oder Zu- und Abschalten von Kreislaufelementen wie Heizungszweig, Zylinderkurbelgehäusekühlung, ATF-Zweig usw., undefinierte Kühlkreislaufzustände auftreten können. Unten ein Beispiel einer instabilen Kühlmittelpumpenkennlinie für einen PKW-Motor (Kennlinien von mir gemessen):
Die Bilder links und rechts zeigen die gleichen Pumpenkennlinien bei unterschiedlichen Drehzahlen, rechts mit Einzelmesswerten. In den Kurvenverläufen ist deutlich ein Strömungsabriss zu erkennen.
Zur Erzielung stabiler Kennlinien können folgende Maßnahmen getroffen werden:
– kleine Schaufelzahl z (damit allerdings größere Minderleistung durch kleineren Minderleistungsfaktor k)
– kleine Schaufelaustrittwinkel ![]()
– Vorziehen der Eintrittskante in den Saugmund
– kleine spezifische Drehzahl ![]()
– kleiner radialer Dichtspalt
– großes Durchmesserverhältnis ![]() (Außendurchmesser Schaufelrad / Eintrittsdurchmesser Schaufelrad; Richtwert
(Außendurchmesser Schaufelrad / Eintrittsdurchmesser Schaufelrad; Richtwert ![]() ungefähr zwischen 2…4)
ungefähr zwischen 2…4)