Die im Flüssigkeitskreislauf zur Verfügung stehende Nutzleistung ![]() der Kühlmittelpumpe errechnet sich aus:
der Kühlmittelpumpe errechnet sich aus:
![]()
Die Nutzleistung der Pumpe ist im ![]() – Diagramm somit die Fläche unter dem Pumpenarbeitspunkt.
– Diagramm somit die Fläche unter dem Pumpenarbeitspunkt.
Die Nutzleistung erhöht sich mit steigender Fluiddichte.
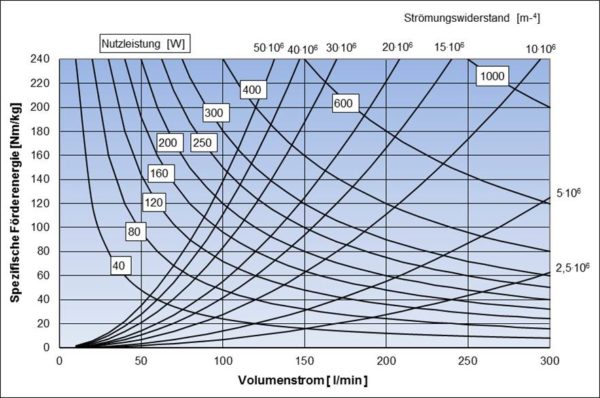
Untenstehendes Bild zeigt die Kurven gleicher Nutzleistung bei üblichen Kühlkreislaufwiderständen:
Die notwendige Pumpenantriebsleistung ![]() wird auf einem entsprechend ausgerüsteten Pumpenprüfstand (s. Kap. 4.4) mit
wird auf einem entsprechend ausgerüsteten Pumpenprüfstand (s. Kap. 4.4) mit
![]()
ermittelt.
Der Gesamtwirkungsgrad der Kühlmittelpumpe ![]() wird aus dem Quotienten aus Nutz- und Antriebsleistung berechnet:
wird aus dem Quotienten aus Nutz- und Antriebsleistung berechnet:
![]()
Hohe Gesamtwirkungsgrade der Kühlmittelpumpe sind oftmals ein Kriterium der Automobilindustrie zur Bestellung einer Pumpe beim Pumpenhersteller. Deshalb soll auf die einzelnen Pumpenwirkungsgrade und die pumpeninternen Verlustleistungen näher eingegangen werden.
Nachfolgendes Schema zeigt die Leistungsbilanz einer Kühlmittelpumpe:
Setzt man in obigem Bild für die Antriebsleistung 100% und trägt prozentual die einzelnen Verlustleistungen an, so erhält man einen Überblick über die relative Größe der einzelnen Verluste und wo bei Verlustleistungsreduzierungen und Wirkungsgradoptimierungen anzusetzen ist. Natürlich lassen sich auch die absoluten Verlustleistungen antragen, falls bekannt.
Für die einzelnen zugeführten und abgeführten Leistungen gilt:
Antriebsleistung:
![]()
mechanische Verlustleistung:
![]()
innere Leistung:
![]()
Leckverlustleistung:
![]()
hydraulische Verlustleistung:
![]()
Radreibungsverlustleistung (nach STODOLA):
![]()
mit
![Rendered by QuickLaTeX.com \[\boldsymbol {\phi =0,8 \cdot \left(\frac{10^{6}}{Re}\right)^{1/6}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-50b13806dda0a00f239765016cc18b8f_l3.png)
und
![]()
Auf einzelne Pumpenleistungen soll hier wegen ihres Einflusses auf den Gesamtwirkungsgrad nochmals näher eingegangen werden:
Antriebsleistung:
Die Pumpenantriebsleistung wird ermittelt, indem auf einem Pumpenprüfstand nach dem Prüfstandsaufbau für Kenngrößenermittlung an Kühlmittelpumpen (s. Kap. 4.4) das Antriebsmoment und die Wellendrehzahl gemessen werden. Dabei ist darauf zu achten, dass wegen der ohnehin kleinen Drehmomente bei Kfz-Kühlmittelpumpen Getriebe- oder Riemenverluste von der Drehmomentmesswelle bis zur Pumpenwelle minimiert bzw. kompensiert werden. Damit werden Fehler bei der Ermittlung von Antriebsleistung und Pumpenwirkungsgrad ausgeschlossen. Bewährt hat sich ein direkter Antrieb der Pumpenwelle mit zwischengeschalteter Messwelle, um Verluste auszuschließen.
Mechanische Verlustleistung:
Die mechanische Verlustleistung einer Kühlmittelpumpe ist die Summe der mechanischen Verluste des Pumpenlagers und der dynamischen Pumpendichtung. Als Pumpendichtungen werden Gleitringdichtungen und Lippen-Dichtungen (VR-Dichtungen) verwendet. Zusätzlich können durch die Drehbewegung der Pumpe Ventilationsverluste auftreten. z.B. an der Riemenscheibe zum Pumpenantrieb.
Leckverlustleistung:
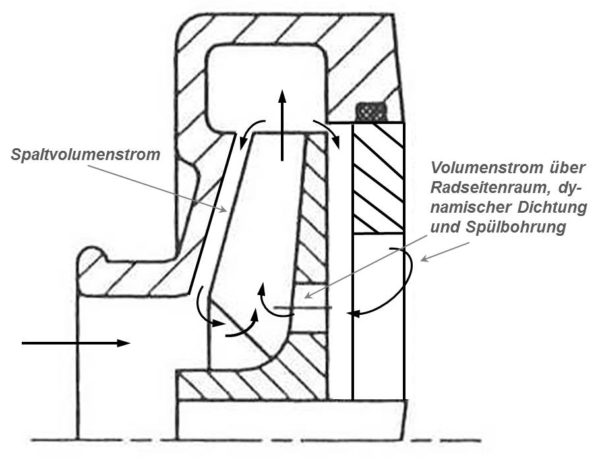
Als Leckagen werden solche Volumenströme bezeichnet, die als Bypass zum Nutzvolumenstrom zur Pumpensaugseite zurückgeführt werden. Leckageverluste sind Leistungsverluste. Für die zu betrachtenden Kfz-Kühlmittelpumpen sind dies die Spaltvolumenströme und die Volumenströme über die Entlastungs- bzw. Spülbohrung. Dabei ist zu beachten, dass die Entlastungs- bzw. Spülbohrungen nicht nur in Saugseitennähe, sondern auch weiter oben in der Schaufel angeordnet sein können. Mit variierender Anordnung entlang des Schaufelkanals kann man unterschiedliche Mengen und Umspülungen von direkt an der Schaufelradrückseite angeordneter Gleitringdichtungen erreichen.
Zu debattieren wäre, ob der Spülvolumenstrom zur Schmierung und Wärmeableitung der im Radseitenraum liegenden Gleitringdichtung wirklich wie per Definition festgelegt einen Leckvolumenstrom darstellt. Die Umspülung der Gleitringdichtung erfüllt eine wichtige Kühlkreislauffunktion. Würde man diesen Spülvolumenstrom dem Nutzvolumenstrom zuschlagen, würde sich der Pumpenwirkungsgrad rein rechnerisch erhöhen, wobei dieser Spülvolumenstrom schwer messtechnisch zu erfassen ist.
Hydraulische Verlustleistung:
Hydraulische Verluste werden durch Reibung sowie Querschnitts- und Richtungsänderungen verursacht. Bei Möglichkeiten zur Wirkungsgradoptimierung wird besonders bei kleinen Schaufelrädern, wie sie im Motorenbau verwendet werden, der Umlenkungsdruckverlust ins Schaufelrad oft ignoriert.
Radreibungsverluste:
Radreibungsverluste treten durch Fluidreibung an den Außenwänden des Schaufelrades auf. Zur Berechnung dieser Radreibungsverluste ist nur die empirische Formel nach Stodola bekannt. Sie ist gegebenenfalls kritisch zu hinterfragen und durch eigene Messungen zu hinterlegen.
Schaufelradwirkungsgrade:
Der Gesamtwirkungsgrad ![]() eines Schaufelrades errechnet sich aus
eines Schaufelrades errechnet sich aus
![]()
und ist gleichzeitig
![]()
Dabei gilt für:
Innerer Wirkungsgrad:
![]()
Hydraulischer Wirkungsgrad:
![]()
Volumetrischer Wirkungsgrad:
![]()
Radreibungswirkungsgrad:
![]()
Mechanischer Wirkungsgrad:
![]()
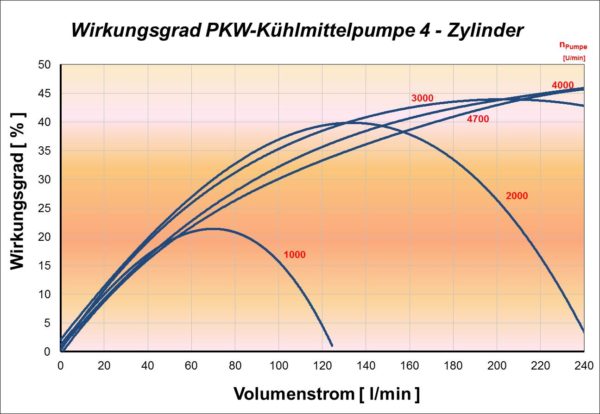
Nachfolgendes Bild zeigt den Wirkungsgradverlauf einer Kfz-Kühlmittelpumpe, ermittelt auf einem Pumpenprüfstand. Die relativ geringen Wirkungsgrade resultieren aus der zu kleinen spezifischen Drehzahl bzw. Laufzahl und der den Einbaubedingungen angepassten Schaufelrad- und Spiralkanalkonstruktion sowie den der Pumpe vor- und nachgeschalteten strömungsungünstigen Zulauf- und Ablaufbedingungen.
Wirkungsgrad von elektrisch angetriebenen Kühlmittelpumpen
Prinzipiell muss zur Ermittlung des Wirkungsgrades einer elektrischen Kühlmittelpumpe der Wirkungsgrad der oben beschriebenen mechanischen Pumpe mit dem Wirkungsgrad des Elektromotors multipliziert werden. Damit erreicht die elektrisch angetriebene Kühlmittelpumpe etwas geringere Wirkungsgrade als die mechanisch angetriebene. Mit einer gemeinsamen Wellenlagerung wird jedoch dabei die Summe der mechanischen Verlustleistungen reduziert.
Besonderes Augenmerk hinsichtlich des Wirkungsgrades ist bei elektrischen Kühlmittelpumpem im Kraftfahrzeug nicht nur auf die eventuell verwendete Hauptpumpe, sondern auch auf die elektrischen Hilfspumpen zu setzen. Oftmals werden zum Beispiel in Plug-in-Fahrzeugen (PHEV) mehrere elektrische Hilfspumpen betrieben. Erfahrungsgemäß laufen diese Pumpen oft in sehr schlechten Wirkungsgradbereichen oder weisen generell schlechte Pumpenwirkungsgrade auf. Damit werden zu ihrem Antrieb hohe Mengen an elektrischer Energie benötigt, was die Reichweite im Batteriebetrieb des Fahrzeuges verringern kann.
Zur Verdeutlichung dieses Problems folgende Beispielrechnung:
Ist-Zustand:
Ansteuerung PVM (Pulsweitenmodulierung) 90%; Wirkungsgrad der el. Hilfspumpe 12%; benötigte elektrische Antriebsleistung 150 Watt.
Optimierte elektrische Hilfspumpe:
Ansteuerung PVM (Pulsweitenmodulierung) 90%; Wirkungsgrad der el. Hilfspumpe 25%; benötigte elektrische Antriebsleistung 72 Watt.
Zu beachten ist, dass die angegebenen Wirkungsgrade für den tatsächlichen Arbeitspunkt und nicht für den am Pumpenprüfstand ermittelten Bestpunkt der Pumpe gelten.
Bei mehreren verwendeten elektrischen Hilfspumpen kann also messbar elektrische Energie eingespart werden, wenn Optimierungsmaßnahmen erfolgen. Diese Optmierungen kann z.B. durch konstruktive Maßnahmen an Schaufelrad und Spiralkanal durch anforderungsgerechte und strömungstechnisch optimale Auslegung erfolgen. Weiterhin können pumpeninterne Verluste (Strömungstrennungen, Strömungsvereinigungen, Spalt, Stoßverluste) minimiert werden und der Spiralkanal strömungstechnisch optimal gestaltet werden.
Bei sehr geringen Volumenströmen sind allerdings hohe Pumpenwirkungsgrade nur schwer zu erreichen.