4.8 Geschwindigkeitsdreieck und Vektordiagramm

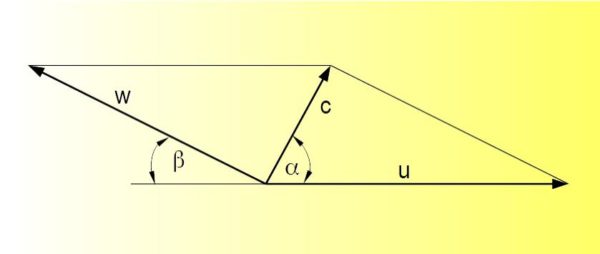
In den vorherigen Kapiteln wurden mitunter schon Geschwindigkeitsdreiecke am Schaufelrad gezeigt, welche hier näher erläutert werden sollen.

Zur Beschreibung der Strömungskinematik im Schaufelrad benutzt man Geschwindigkeitspläne, insbesondere für den Verlauf am Radeintritt und -austritt. Wir betrachten dabei ein radiales Schaufelrad einer Strömungsarbeitsmaschine, welches von innen nach außen durchströmt wird.

Es werden drei Geschwindigkeiten unterschieden:

  • Absolutgeschwindigkeit c
  • Umfangsgeschwindigkeit u
  • Relativgeschwindigkeit w

Die Winkel werden bezeichnet mit:

  • Winkel der Absolutströmung 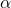\alpha (Winkel zwischen c und u)
  • Winkel der Relativströmung β (Winkel zwischen w und u)

Die Geschwindigkeiten am Schaufelradeintritt werden mit dem Index 1 und am Schaufelradaustritt mit dem Index 2 gekennzeichnet. Zusätzlich werden zur präziseren Erläuterung der Verhältnisse wegen der endlichen Dicke der Schaufeln die Stelle unmittelbar vor dem Schaufelradeintritt mit 0 und die Stelle unmittelbar nach dem Schaufelradaustritt mit der Stelle 3 bezeichnet. Die Umfangsgeschwindigkeit ist an allen Stellen von der Schaufelversperrung unbeeinflusst, deshalb gilt u_0 = u_1 und u_2 = u_3. Absolutgeschwindigkeit c und Relativgeschwindigkeit w ändern sich durch den Schaufeldickeneinfluss.

Stellt man sich vor, dass man von außen auf die radiale Strömung im Schaufelrad schauen würde, dann beobachtet man eine bestimmte Geschwindigkeit der Durchströmung von innen nach außen, dies ist die absolute Geschwindigkeit c. Die gleiche Beobachtungsperspektive  würde weiterhin ergeben, dass sich jeder Punkt des rotierenden Schaufelrades mit einer bestimmten Geschwindigkeit bewegt, der Umfangsgeschwindigkeit u. Stellt man sich weiterhin vor, man würde im Schaufelkanal stehen und die Strömung auf sich zu- oder wegströmen sehen, dann ist dies die relative Geschwindigkeit w.

An eine Schaufel, im Bild unten für den Schaufeleintritt, gezeichnet, ergeben sich wie im Bild unten links dargestellt folgende Geschwindigkeiten:

Aus den Geschwindigkeiten an einem beliebigen Punkt der Schaufel werden Geswchwindigkeitsparallelogramme gebildet (oben Bild rechts). Für die Berechnungen am Schaufelrad ergeben sich aus diesen Geschwindigkeitsparallelogrammen die unten dargestellten Geschwindigkeitsdreiecke für Eintritt und Austritt inklusive Schaufelwinkel:

Bei Antragen der Geswchwindigkeitsdreiecke an Eintritt und Austritt am Schaufelrad ergeben sich folgende Verhältnisse:

formelzeichen 4 8

Die Relativgeschwindigkeit w stimmt in etwa mit der Schaufelrichtung überein. Die Absolutgeschwindigkeit c ist die geometrische Summe aus Umfangsgeschwindigkeit u und Relativgeschwindigkeit w:

    \[\boldsymbol {\vec{c}=\vec{u}+\vec{w}}\]

Die Umfangsgeschwindigkeit u ergibt sich aus dem Radius r und der Winkelgeschwindigkeit ω:

    \[\boldsymbol {u=r\cdot \omega=D\cdot\pi\cdot n}\]

Absolutgeschwindigkeit c und Relativgeschwindigkeit w können in ihre Komponenten zerlegt werden:

a) in die Meridiankomponenten c_m und w_m:
Es gilt c_m=w_m. Die Meridianrichtung steht senkrecht auf der Umfangsrichtung. Die Meridiangeschwindigkeit kann als geometrische Summe aus Axialgeschwindigkeit und Radialgeschwindigkeit aufgefasst werden, Bild oben rechts.

Die Meridiankomponente berechnet sich aus der Kontinuitätsgleichung:

    \[\boldsymbol {c_{m}=\frac{Volumenstrom}{Querschnittsfl\"ache}}\]

    \[\boldsymbol {c_{m1}=k_{1}\cdot\frac{\dot{V}}{\pi\cdot D_{1}\cdot b_{1}}}\]

    \[\boldsymbol {c_{m2}=k_{2}\cdot\frac{\dot{V}}{\pi\cdot D_{2}\cdot b_{2}}}\]

Die Verengungsfaktoren k1 und k2 berücksichtigen den Einfluss der Schaufeldicke und sind >1. Berechnungsvorschriften dazu unter 4.11.

b) in die Umfangskomponenten c_u und w_u:
Die Umfangskomponente wird über den Energieumsatz am Schaufelrad bestimmt. Im Auslegungspunkt soll  drallfreie Zuströmung vorliegen. Damit und aus der Eulerschen Strömungsmaschinen-Hauptgleichung wird:

    \[\boldsymbol {c_{u1}=0}}\]

    \[\boldsymbol {c_{u2}=\frac{Y_{th\,\infty}}{u_{2}}}\]

nächstes Kapitel