1. Allgemeine Betrachtungen nach Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg
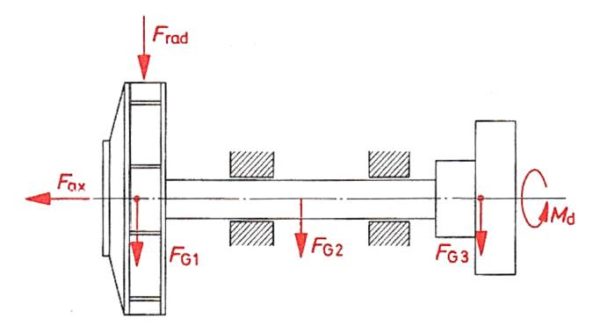
Zur Berechnung der Pumpenwelle und der Lager werden die Kräfte und Momente, die am Schaufelrad, an der Welle und ggf. an anderen angebrachten Maschinenelementen wie z.B. Kupplungen oder Antriebsscheiben angreifen, benötigt. Untenstehend sind die Kräfte an einer Welle mit Schaufelrad dargestellt:
Dabei werden folgende Kräfte und Momente unterschieden:
- Gewichtskräfte
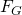 aus Schaufelradgewichten, Wellengewicht, Gewichte von aufgesetzten Maschinenteilen
aus Schaufelradgewichten, Wellengewicht, Gewichte von aufgesetzten Maschinenteilen - Axialschub
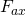 in Richtung Schaufelradsaugseite
in Richtung Schaufelradsaugseite - Radialschub
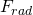
- Unwuchtkräfte
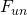
- Riemenzug oder Zahnkräfte
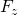
- übertragenes Drehmoment
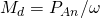
Nachfolgend werden einige Aspekte von Axialschub, Radialschub und biegekritischer Drehzahl betrachtet. Für weitergehende Untersuchungen kann die einschlägige Fachliteratur verwendet werden.
2. Axialschub – Berechnung der Axialkräfte am Schaufelrad
Da der Axialschub neben der Lagerausführung auch einen erheblichen Einfluss auf die Gestaltung des Schaufelrades hat, ist eine entsprechende Vorabschätzung der Axialkräfte erforderlich. Besonders beim Einsatz von Kunststoffen kann es auch zu Durchbiegungen der Tragscheibe des Schaufelrades und somit zum Anlaufen des Rades am Pumpengehäuse oder am Motorgehäuse kommen. Man sollte daher für solche Spezialfälle eine entsprechende Axialkraftberechnung durchführen.
Es ist zu beachten, dass bei den Kfz- Kühlmittelpumpen sowohl geschlossene als auch halboffene und offene Schaufelräder zum Einsatz gelangen.
Bei offenen Schaufelrädern wird die Axialkraft größer als bei geschlossenen Rädern, weil der Druck im schaufellosen Radseitenraum grundsätzlich über den Druck im Schaufelrad liegt. Man könnte den Axialschub wieder durch Rückenschaufeln am Schaufelrad reduzieren. Dies ist jedoch für die Kühlung und Umspülung der dynamischen Pumpenabdichtung im Dichtungsbereich nachteilig.
Eine Schubreduzierung lässt sich durch Aussparungen in der Tragscheibe erreichen.
2.1 Axialschub – Berechnung nach Gülich, J.F: Kreiselpumpen, Springer Verlag 1999
Eine Überschlagsberechnung kann mit folgender Formel erfolgen:
![]()
Mit ![]() = Durchmesser des radialen Spaltes und
= Durchmesser des radialen Spaltes und ![]() = Dichtungsdurchmesser.
= Dichtungsdurchmesser.
Weiter Ausführung zu den Axialschüben können dem Fachbuch entnommen werden.
2.2 Axialschub – Berechnung nach Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg
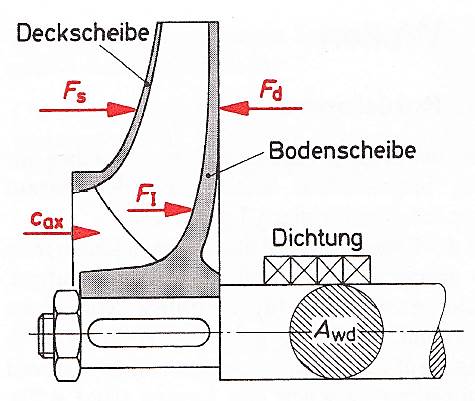
Die exakte Berechnung des Axialschubes ist nach Bohl/Elmendorf sehr schwierig, da er sich aus der Summe aller statischen und dynamischen Axialkräfte zusammensetzt. Neben den Strömungskräften können auch Axialkräfte durch Gewichtskräfte bei nichthorizontalem Einbau, durch Zahnradkräfte bei schrägverzahnten Zahnrädern, durch Dichtungskräfte und anderen Ursachen auftreten. Hier sollen nur die Strömungskräfte betrachtet werden.
Bei Radialrädern ergibt sich:
![]()
Die Druckkraft ![]() ergibt sich aus:
ergibt sich aus:
![]()
![]() ist die Druckkraft auf die Bodenscheibe und
ist die Druckkraft auf die Bodenscheibe und ![]() die Druckkraft auf die Deckscheibe.
die Druckkraft auf die Deckscheibe.
Die Impulskraft ![]() ergibt sich aus:
ergibt sich aus:
![]()
![]() ist die Differenz der Axialkomponenten der Absolutgeschwindigkeit am Schaufelradeintritt und -austritt.
ist die Differenz der Axialkomponenten der Absolutgeschwindigkeit am Schaufelradeintritt und -austritt.
Die Wellendichtungskraft ![]() ergibt sich aus:
ergibt sich aus:
![]()
![]() ist der Wellenquerschnitt und
ist der Wellenquerschnitt und ![]() der Druckunterschied vor und hinter der Wellendichtung.
der Druckunterschied vor und hinter der Wellendichtung.
![]() sind z.B. Zahnradkraft, Rotorgewicht bei nicht horizontalem Einbau, magnetischer Zug bei direkt angebauten Elektromotoren u.a.
sind z.B. Zahnradkraft, Rotorgewicht bei nicht horizontalem Einbau, magnetischer Zug bei direkt angebauten Elektromotoren u.a.
In Bohl/Elmendorf wird folgende empirische Formel der Fa. KSB zur Abschätzung der größten Komponente des Axialschubes, der Druckkraft ![]() angegeben:
angegeben:
![]()
![]() ist die nicht entlastete Schaufelradfläche, d.h. die Fläche mit unterschiedlichen Drücken auf Boden- und Deckscheibe.
ist die nicht entlastete Schaufelradfläche, d.h. die Fläche mit unterschiedlichen Drücken auf Boden- und Deckscheibe.
Für Diagonal- und Axialräder wird von KSB folgende Formel vorgeschlagen:
![]()
![]() ist der Schaufelradaußendurchmesser.
ist der Schaufelradaußendurchmesser.
Der durch Strömungskräfte und Druckunterschiede nicht ausgeglichene erzeugte Schub muss vom Festlager aufgenommen werden. Zur Absenkung des Axialschubes können folgende Maßnahmen ergriffen werden:
1. Gegenläufige Anordnung von Schaufelrädern (für Kraftfahrzeugpumpen nicht relevant).
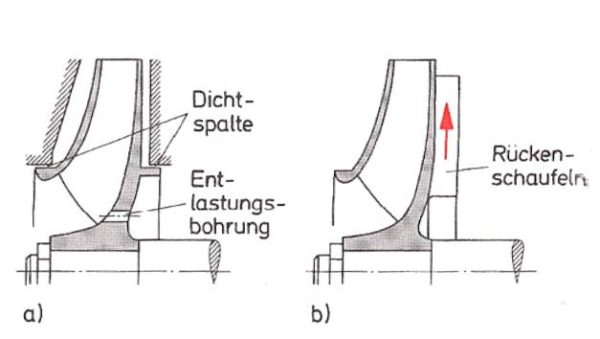
2. Anbringen eines druckseitigen Dichtspaltes kombiniert mit Entlastungsbohrungen, unten Bild a.
3. Anbringen von Rückenschaufeln, unten Bild b.
4. Anbringen von Ausgleichskolben oder Entlastungsscheibe
5. geschlossenes statt offenes Schaufelrad
3. Radialschub nach Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg
Der Radialschub ist eine am Schaufelrad angreifende radiale Kraft, die durch die Wechselwirkung von Strömungskräften zwischen Schaufelrad und Gehäuse entsteht. Es werden stationäre Radialkräfte, deren Größe und Richtung vom Verhältnis des jeweiligen Volumenstromes zum Auslegungsvolumenstrom abhängt, und instationäre Radialkräfte mit zeitlich veränderlichen Größen und Richtungen unterschieden.
Für einfache Spiralgehäusepumpen wird folgende Überschlagsformel empfohlen:
![]()
Die Radialschubkoeffizienten ![]() steigen mit Entfernung des Radvolumenstromes vom Optimalpunkt stark an und können aus in Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg dagestellten Kurvenverläufen für spezifische Drehzahlen zwischen 10 und 60
steigen mit Entfernung des Radvolumenstromes vom Optimalpunkt stark an und können aus in Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg dagestellten Kurvenverläufen für spezifische Drehzahlen zwischen 10 und 60 ![]() abgelesen werden.
abgelesen werden.
4. Biegekritische Drehzahl nach Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg
Eine Gesamtbetrachtung zur Ermittlung der biegekritischen Drehzahl soll hier wegen ihrer Komplexität nicht durchgeführt werden. Es wird vorgeschlagen, bei notwendigen genaueren Betrachtungen zu biegekritischen Drehzahlen, z.B. bei größeren Nfz-Pumpen, Literatur wie beispielsweise Bohl/Elmendorf: Strömungsmaschinen I und II, Vogel Buchverlag Würzburg (nachfolgend als Bohl/Elmendorf bezeichnet) und darin aufgelistete weiterführende Literatur zu nutzen. Eine kurze Einführung in die Problematik soll an dieser Stelle das Grundverständnis zu möglichen auftretenden Problemen erhöhen.
Die biegekritische Drehzahl des Rotors sind die Drehzahlen, bei denen die Durchbiegung der Welle unzulässig hohe Werte annimmt und es zum Anstreifen des Rotors an die Gehäusewand kommt. Die Durchbiegung der Welle geht dabei z.B. von kleineren Unwuchten aus.
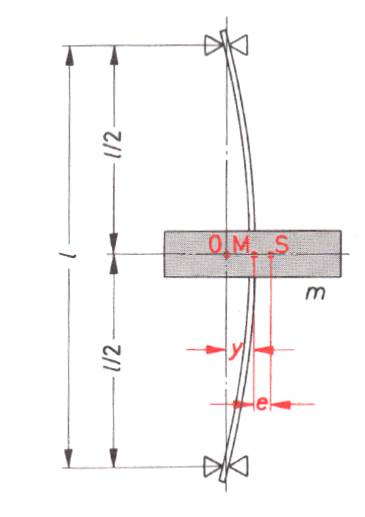
Zur Erklärung der biegekritischen Drehzahl wird zunächst ein sehr einfacher Rotor, siehe untenstehendes Bild, bestehend aus einer masselosen Welle und einer mittig angebrachten Scheibe mit der Masse m betrachtet:
Der Scheibenschwerpunkt S liegt um die Exzentrizität e außerhalb des Mittelpunktes, wodurch eine Unwuchtkraft von der Größe
![]()
auftritt. 0 ist der Ruhemittelpunkt. Der Unwuchtkraft wirkt eine der Federsteifigkeit der Welle entsprechende Rückstellkraft entgegen (c ist die Federsteife der Welle und y die Wellenauslenkung in Wellenmitte):
![]()
Durch Gleichsetzen von ![]() und
und ![]() und Unformen erhält man die Grundbeziehung für die biegekritische Drehzahl:
und Unformen erhält man die Grundbeziehung für die biegekritische Drehzahl:
![]()
Für e ungleich 0 geht die Wellenauslenkung y gegen unendlich, wenn c/m = ![]() wird. Diesen Zustand bezeichnet man als Resonanz, die Kreisfrequenz ω wird gleich der Biegeeigenfrequenz der Welle:
wird. Diesen Zustand bezeichnet man als Resonanz, die Kreisfrequenz ω wird gleich der Biegeeigenfrequenz der Welle:
![]()
Die Beziehungen zum unter- und überkritischen Bereich können aus Bohl/Elmendorf entnommen werden.
Die Welle muss so ausgelegt sein, dass Resonanz vermieden wird, d.h. der Bereich um ![]() = 1 nicht oder nur kurzzeitig auftritt.
= 1 nicht oder nur kurzzeitig auftritt.
Zur überschlägigen Ermittlung der biegekritischen Drehzahl wird das Verfahren nach DUNKERLEY vorgeschlagen, für andere und genauere Verfahren sind Bohl/Elmendorf und die weiterführenden Literaturhinweise heranzuziehen.
Zunächst werden die biegekritischen Drehzahlen für Wellen mit Einzelmassen bzw. ohne aufgesetzte Massen folgendermaßen berechnet (weitere Wellen- bzw. Rotoranordnungen und die zugehörigen Berechnungsvorschriften in Bohl/Elmendorf):
Zunächst die Berechnung für eine masselose Welle mit Einzelmasse:
![Rendered by QuickLaTeX.com \[\boldsymbol {\omega_{kr}=\sqrt{\frac{3\cdot E \cdot I}{m\left(l+c\right)\cdot c^{2}}}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-00049dc519134e28ba6a7a3d55c424d3_l3.png)
E = Elastizitätsmodul der Welle, ![]() = Trägheitsmoment der Welle.
= Trägheitsmoment der Welle.
Dann die Berechnungen der Wellenabschnitte ohne Einzelmasse:
Bei dem oben abgebildete Rotor gilt zwischen den Lagern als Welle ohne Einzelmasse für die Berechnung der biegekritischen Eigenfrequenz 1.Ordnung:
![Rendered by QuickLaTeX.com \[\boldsymbol {\omega_{kr}=\frac{2.47}{I^2}\cdot d \cdot \sqrt{\frac{E}{\varrho}}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-d749db2d3f3b0c26526bf91c3125e697_l3.png)
Bei dem oben abgebildete Rotor gilt vom Lagern bis zum Schaufelrad als Welle ohne Einzelmasse für die Berechnung der biegekritischen Eigenfrequenz 1.Ordnung:
![Rendered by QuickLaTeX.com \[\boldsymbol {\omega_{kr}=\frac{0,88}{I^2}\cdot d \cdot \sqrt{\frac{E}{\varrho}}}\]](http://igszwickau.de/wp-content/ql-cache/quicklatex.com-f0e7a60d3c72395d9add773506b948d3_l3.png)
Zur Berechnung der biegekritischen Drehzahl des Gesamtrotors inkl. Wellenabschnitte werden die einzelnen biegekritischen Drehzahlen, ermittelt nach obigen Vorschriften, eingesetzt:
![]()
Die biegekritische Drehzahl wird durch Umformung der Federsteife und der Masse zu:
![]()
Damit kann nach vorheriger Berechnung der biegekritischen Drehzahl die Auslenkung der Welle y ermittelt werden.
In Bohl/Elmendorf ist ein Berechnungsbeispiel aufgeführt, dessen Skizze gut zu den in Kraftfahrzeugen verwendeten radialen Pumpen passt. Dieses Berechnungsbeispiel kann als Vorlage zur Bestimmung der biegekritischen Drehzahlen dienen.